Cho x, y thỏa mãn : 8x + 9y = 48. Tìm giá trị lớn nhất của tích P = xy.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

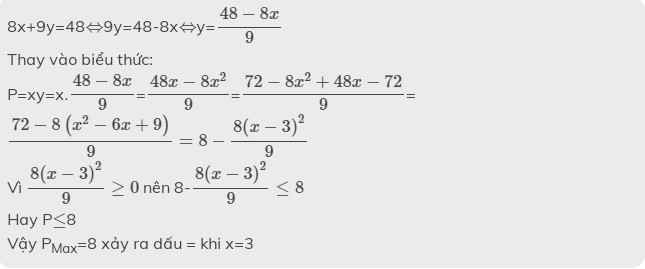

a) \(6xy+4x-9y-7=0\)
\(\Leftrightarrow2x.\left(3y+2\right)-9y-6-1=0\)
\(\Leftrightarrow2x.\left(3y+x\right)-3.\left(3y+2\right)=1\)
\(\Leftrightarrow\left(2x-3\right).\left(3y+2\right)=1\)
Mà \(x,y\in Z\Rightarrow2x-3;3y+2\in Z\)
Tự làm típ
\(A=x^3+y^3+xy\)
\(A=\left(x+y\right)\left(x^2-xy+y^2\right)+xy\)
\(A=x^2-xy+y^2+xy\)( vì \(x+y=1\))
\(A=x^2+y^2\)
Áp dụng bất đẳng thức Bunhiakovxky ta có :
\(\left(1^2+1^2\right)\left(x^2+y^2\right)\ge\left(x\cdot1+y\cdot1\right)^2=\left(x+y\right)^2=1\)
\(\Leftrightarrow2\left(x^2+y^2\right)\ge1\)
\(\Leftrightarrow x^2+y^2\ge\frac{1}{2}\)
Hay \(x^3+y^3+xy\ge\frac{1}{2}\)
Dấu "=" xảy ra \(\Leftrightarrow x=y=\frac{1}{2}\)

\(4x^2-2+\frac{1}{4x^2}+\left(2x\right)^2+y^2=4\)
\(\left(\left(2x\right)^2-\frac{1}{\left(2x\right)^2}\right)^2+\left(\left(2x\right)-y\right)^2=4-2\left(2x\right)y\)
\(VT\ge0\) đẳng thức khi: 2x=+-1; 2x=y;
\(\Rightarrow4-4xy\ge0\Rightarrow xy\le1\)
DS: x=+-1/2; y+-1

\(\left(x-y\right)^2\ge0\)
\(\Rightarrow\left(x+y\right)^2\ge4xy\)
\(\Rightarrow xy\le\dfrac{\left(x+y\right)^2}{4}=\dfrac{2019^2}{4}\)
Dấu = xảy ra khi \(x=y=\dfrac{2019}{2}\)

A = xy + 2yz + 3xz = xy + xz + 2yz + 2xz = x(y + z) + 2z(y + z)
Áp dụng BĐT: (a+b)^2/4 ≥ ab dấu = khi a = b
ta có:
(x + y + z)^2/4 ≥ x(y + z)
(x+ y +z)^2/4 ≥ z(y + z)
=> A ≤ 3(x + y + z)^2/4 = 3.36/4 = 27
=>Giá trị lớn nhất của = 27 sẽ xảy ra khi có các trường hợp:
{x = y + z
{z = y + z
Vậy y = 0 và x = z = 3
\(A=xy+2yz+3zx=x\left(6-x-z\right)+2\left(6-x-z\right)+3zx\)
\(=-x^2+6x-2z^2+12z=\left(-x^2+6x-9\right)+\left(-2z^2+12z-18\right)+27\)
\(=27-\left(x-3\right)^2-2\left(z-3\right)^2\le27\)

với mọi x, y, z ta có:
(x-y)^2 +(y-z)^2+ (z-x)^2>=0
<=>2x^2 +2y^2 + 2z^2 - 2xy -2yz - 2xz >=0
<=>x^2 + y^2 +z^2 - xy -yz -zx >=0
<=>(x+y+z)^2 >= 3(x+y+z)
<=>[(x+y+z)^2]/3 >= xy+yz+ zx
=>xy +yz + zx <=3
dấu = xảy ra khi x=y=z =1
ai tích mình tích lại nhưng phải lên điểm mình tích gấp đôi

Lời giải:
$x^2-x^2y-y+8x+7=0$
$\Leftrightarrow x^2+8x+7=y(x^2+1)$
$\Leftrightarrow y=\frac{x^2+8x+7}{x^2+1}$
$\Leftrightarrow y=\frac{(x^2+1)+8x+6}{x^2+1}=1+\frac{8x+6}{x^2+1}$
Áp dụng bđt AM-GM ta có:
$x^2+\frac{1}{4}\geq |x|\geq x$
$\Rightarrow x^2+1\geq x+\frac{3}{4}=\frac{4x+3}{4}$
$\Rightarrow \frac{8x+6}{x^2+1}\leq \frac{2(4x+3)}{\frac{4x+3}{4}}=8$
$\Rightarrow y\leq 1+8=9$
Vậy $y_{\max}=9$
$x^2=\frac{1}{4}$; $x\geq 0\Rightarrow x=\frac{1}{2}$
pt\(\Leftrightarrow x^2\left(1-y\right)+8x+7-y=0\) (1)
Ta có :\(\Delta\)(x)=\(-y^2+8y+9\)(do làm biếng nên làm ra denta luôn)
Để tồn tại MAX y thì PT (1) có ngiệm nên \(\Delta\ge0\) \(\Leftrightarrow-y^2+8y+9\ge0\)
\(\Leftrightarrow-y^2-y+9y+9\ge0\Leftrightarrow-y\left(y+1\right)+9\left(y+1\right)\ge0\)
\(\Leftrightarrow\left(y+1\right)\left(9-y\right)\ge0\)
Giải BPT ta được : \(-1\le y\le9\)
\(\Rightarrow\) Max y =9. Thay y=9 vào (1)\(\Rightarrow x=\dfrac{1}{2}\)
Vậy Max y=9\(\Leftrightarrow x=\dfrac{1}{2}\)

từ giả thiết ta có : z = 6 - x - y
Ta có : \(A=xy+z\left(2y+3x\right)=xy+\left(6-x-y\right)\left(2y+3x\right)\)
\(=-3x^2-2y^2-4xy+18x+12y\)
Do đó : \(3A=-9x^2-6y^2-12xy+54x+36y=-9x^2-6x\left(2y-9\right)-6y^2+36y\)
\(=-\left(3x+2y-9\right)^2-2y^2+81\le81\)
\(\Rightarrow A\le27\)
Vậy giá trị lớn nhất của A là 27 \(\Leftrightarrow\hept{\begin{cases}3x+2y-9=0\\y=0\end{cases}\Leftrightarrow x=3;y=0;z=3}\)