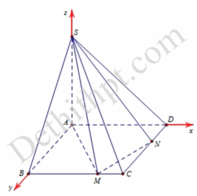
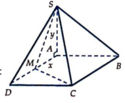
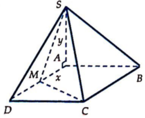
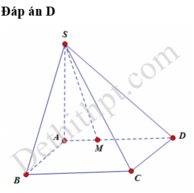
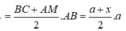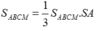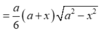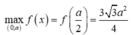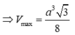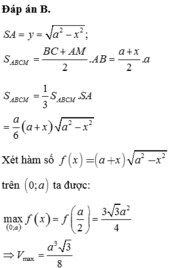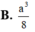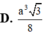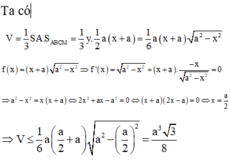Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a, cạnh bên SA vuông với đáy. Trên cạnh BC lấy điểm M di động và cạnh CD lấy N di động sao cho góc MAN=45 độ. Gọi BM=x, DN=y và (0<x;y<a)
Chứng minh a(x+y)=a2-xy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 2 2021
Dựng CH _|_ AB => CH _|_ (SAB)
Giả sử MN cắt AD tại F. Theo định lý Talet ta có:
\(\frac{DF}{MC}=\frac{ND}{NC}=\frac{1}{2}\Rightarrow DF=\frac{MC}{2}=\frac{a}{4}\)
Khi đó \(\frac{PA}{PC}=\frac{AF}{MC}=\frac{5}{2}\Rightarrow\frac{CA}{PA}=\frac{7}{5}\)
Do đó: d (P;(SAB))=\(\frac{5}{7}d\left(C;\left(SAB\right)\right)=\frac{5}{7}CH=\frac{5}{7}\cdot\frac{a\sqrt{3}}{2}=\frac{5a\sqrt{3}}{14}\)
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 8 2021
Chi tiết \(BM=DN=\dfrac{a}{3}\) hoàn toàn không cần thiết
a.
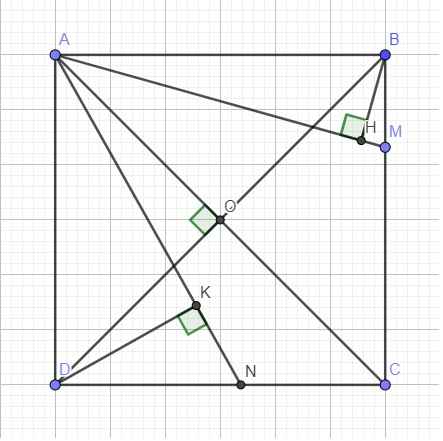
Ta có: \(AC\perp BD\) tại O (2 đường chéo hình vuông) \(\Rightarrow O\) thuộc đường tròn đường kính AB
\(AH\perp BH\) (gt) \(\Rightarrow\) H thuộc đường tròn đường kính AB
\(\Rightarrow\) 4 điểm A,B,O,H cùng thuộc đường tròn đường kính AB hay tứ giác ABHO nội tiếp
Hoàn toàn tương tự, 4 điểm ADKO cùng thuộc đường tròn đường kính AD nên tứ giác ADKO nội tiếp
b.
Trong tam giác vuông ABM vuông tại B với đường cao BH, áp dụng hệ thức lượng:
\(AB^2=AH.AM\)
Tương tự, trong tam giác vuông ADN:
\(AD^2=AK.AN\)
Mà \(AB=AD=a\Rightarrow AH.AM=AK.AN\Rightarrow\dfrac{AH}{AN}=\dfrac{AK}{AM}\) (đpcm)
CM
20 tháng 12 2018
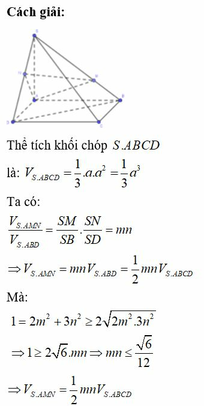
Đáp án B
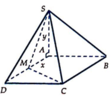
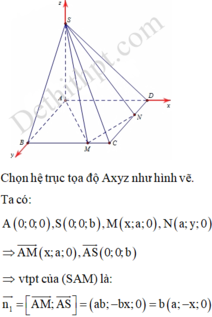
S A = y = a 2 - x 2 ; S A B C M = B C + A M 2 . A B = a + x 2 . a
S A B C M = 1 3 S A B C M . S A = a 6 ( a + x ) a 2 - x 2
Xét hàm số f ( x ) = ( a + x ) a 2 - x 2 trên 0 ; a ta được:
m a x 0 ; a f ( x ) = f a 2 = 3 3 a 2 4 ⇒ V m a x = a 3 3 8
trên (0;a) ta được:
