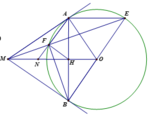
Cho đường tròn tâm O.Từ điểm E ở ngoài đường tròn kẻ hai tiếp tuyến EM và EN (M và N là các tiếp điểm).OE cắt MN tại H.
a)Chứng minh OE vuông góc với MN.
b)Vẽ đường kính NOB .Chứng minh OBMH là hình thang.
c)Cho ON=2cm và OE=4 cm .Tính độ dài các cạnh và diện tích tam giác EMN.


a: Xét (O) có
EM là tiếp tuyến
EN là tiếp tuyến
Do đó:EM=EN
mà OM=ON
nên OE là đường trung trực của MN
=>OE\(\perp\)MN(1)
b: Xét (O) có
ΔNMB nội tiếp
NB là đường kính
Do đó: ΔNBM vuông tại M
=>NM\(\perp\)MB(2)
=>NB//OH
hay OHMB là hình thang