Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
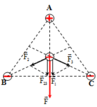
Lực điện tổng hợp tác dụng lên q 0 là: F → = F → 1 + F → 2 + F → 3 = F → 1 + F → 23
Trong đó: F 1 = k q 1 q 0 A O 2 = k q 1 q 0 2 3 a 3 2 2 = 3 k q 1 q 0 a 2 = 36.10 5
Vì BO = AO = CO nên q 1 = q 2 = q 3 → F 1 = F 2 = F 3
F → 2 ; F → 3 = 120 0 → F 1 = F 23
Tam giác ABC vuông tại C vì A B 2 = A C 2 + B C 2
Các điện tích q 1 v à q 2 gây ra tại C các véc tơ cường độ điện trường E 1 → và E 2 → có phương chiều như hình vẽ.
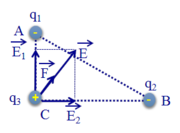
Có độ lớn: E 1 = k | q 1 | A C 2 = 9.10 9 .8.10 − 6 0 , 24 2 = 12 , 5 . 10 5 (V/m);
E 2 = k | q 2 | B C 2 = 9.10 9 .6.10 − 6 0 , 18 2 = 16 , 7 . 10 5 (V/m);
Cường độ điện trường tổng hợp tại C là:
E → = E 1 → + E 2 → có phương chiều như hình vẽ, có độ lớn:
E = E 1 2 + E 2 2 = ( 12 , 5.10 5 ) 2 + ( 16 , 7.10 5 ) 2 = 20 , 7 . 10 5 (V/m).
F → = q 3 . E → ; vì q 3 > 0 nên F → cùng phương cùng chiều với E → và có độ lớn:
F = q 3 E = 9 . 10 - 6 . 20 , 7 . 10 5 = 18 , 6 ( N ) .
Lực tổng hợp tác dụng lên q0 :
\(\overrightarrow{F}=\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}\)
Trong đó :
\(F_1=k\dfrac{\left|q_1q_0\right|}{AO^2}=k.\dfrac{\left|q_1q_0\right|}{\left(\dfrac{2}{3}a\dfrac{\sqrt{3}}{2}\right)^2}=3k\dfrac{\left|q_1q_2\right|}{a^2}=36.10^{-5}N\)
Vì BO = CO = AO , \(\left|q_2\right|=\left|q_3\right|=\left|q_1\right|\)nên
F2 = F3 = F1
Đặt \(\overrightarrow{F'}=\overrightarrow{F_2}+\overrightarrow{F_3}\)
=> \(\overrightarrow{F}=\overrightarrow{F_1}+\overrightarrow{F'}\)
Vì F2 = F3 và \(\left(\overrightarrow{F_2},\overrightarrow{F_3}\right)\)= 120o
Nên F' = F2 = F3 và F' nằm trên phân giác \(\widehat{BOC}\)
Vì \(\overrightarrow{F_1},\overrightarrow{F'}\)cùng chiều nên
* F = F1+ F' = 72.10-5N
* \(\overrightarrow{F}\)nằm trên AO chiều ra xa A