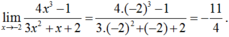24x3-2+89x6+58-31
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




72 + 36 x 2 + 24 x 3 + 18 x 4 + 12 x 6 + 168
= 72 + 72 + 72 + 72 + 72 + 168
= ( 72 x 5 ) + 168
= 360 + 168
= 528
chúc bạn học tốt

Ta có thể viết lại A và B dưới dạng:
A = 29!
B = (58!/29!) / 30
Ta sẽ chứng minh rằng A + B chia hết cho 59 bằng cách chứng minh rằng A ≡ -B (mod 59).
Đầu tiên, ta áp dụng định lý Wilson: (p-1)! ≡ -1 (mod p) nếu p là số nguyên tố. Áp dụng định lý này với p = 59, ta có:
58! ≡ -1 (mod 59)
Ta nhân cả hai vế của phương trình trên với 29!, ta được:
29!(58!) ≡ -29! (mod 59)
Nhưng ta biết rằng 29! ≡ A (mod 59) và (58!/29!) ≡ B (mod 59), do đó ta có:
A * B ≡ -A (mod 59)
Thêm A vào cả hai vế của phương trình, ta được:
A + A * B ≡ 0 (mod 59)
Nhưng ta biết rằng A + B = 29! + (58!/29!) / 30, do đó:
A + B ≡ A + A * B (mod 59)
Vậy ta kết luận được rằng A + B chia hết cho 59.

\(a,24\times4+24\times3+24\times2\)
\(=24\times\left(4+3+2\right)\)
\(=24\times9\)
\(=216\)
\(b,2007\times16-2007\times14-2007\times2+2007\)
\(=2007\times\left(16-14-2+1\right)\)
\(=2017\times1\)
\(=2017\)
a, 24 x ( 4 + 3 + 2 ) = 24 x 9 = 216
b, 2007 x 16 - 14 - 2 + 1 ) = 2007 x 1 = 2007