Bạn @Huỳnh Yến,giúp mk bài này nghen,bn khác cũng được
1/Cho ΔABC có AB=AC.Lấy điểm H thuộc cạnh AC và điểm K thuộc cạnh AB sao cho AH=AK.Gọi O là giao điểm của BH và CK.Chứng minh:
a,BH=CK
b,ΔOBK=ΔOCH
c, AO là tia phân giác của góc A
d,Gọi I là trung điểm của BC.Chứng minh:3 điểm A,O,I thẳng hàng

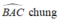

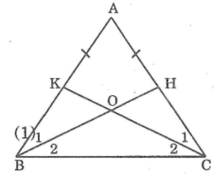
Hình minh họa: O A B C H K I 1 1 2 2 1 1
Bài làm:
a, Xét \(\Delta ABH\) và \(\Delta ACK\)
AB = AC (gt)
\(\widehat{A}\): chung
AH = AK (gt)
=> \(\Delta ABH=\Delta ACK\left(c-g-c\right)\)
=> BH = CK (đpcm)
b, Ta có: AK + BK = AB
AH + CH = AC
mà AH = AK (gt) ; AB = AC (gt)
=> BK = CH
Có: \(\widehat{H_1}=\widehat{K_1}\left(\Delta ABH=\Delta ACK\right)\)
=> \(\widehat{H_2}=\widehat{K_2}\)
Xét \(\Delta OBK\) và \(\Delta OCH\) có:
\(\widehat{K_2}=\widehat{H_2}\left(cmt\right)\)
BK = CH (cmt)
\(\widehat{B_1}=\widehat{C_1}\left(\Delta ABH=\Delta ACK\right)\)
=> \(\Delta OBK=\Delta OCH\left(g-c-g\right)\rightarrowđpcm\)
c, Xét \(\Delta AOB\) và \(\Delta AOC\) có:
AB = AC (gt)
AO: chung
OB = OC (\(\Delta OBK=\Delta OCH\))
\(\Rightarrow\Delta AOB=\Delta AOC\left(c-c-c\right)\)
\(\Rightarrow\widehat{BAO}=\widehat{CAO}\) mà O nằm trong tam giác ABC
=> AO là tia p/g của góc A --> đpcm
d, Xét \(\Delta ABI\) và \(\Delta ACI\):
AB = AC (gt)
AI: chung
BI = CI (gt)
\(\Rightarrow\Delta ABI=\Delta ACI\left(c-c-c\right)\)
\(\Rightarrow\widehat{BAI}=\widehat{CAI}\) => AI là tia p/g của góc A
mà AO cx là tia p/g của góc A
=> AO trung AI
=> 3 điểm A, O, I thẳng hàng --> đpcm
(Hình ảnh minh họa)
A H C K B O I 1 2 1 2 1 2 1 2
a) *Xét ΔAHB và ΔAKC có:
\(\left\{{}\begin{matrix}AB=AC\left(gt\right)\\\widehat{A}.l\text{à}.g\text{óc}.chung\\AH=AK\left(gt\right)\end{matrix}\right.\)
⇒ ΔAHB = ΔAKC (c - g - c)
⇒ BH = CK (hai cạnh tương ứng)
b) *Vì ΔAHB = ΔAKC (cmt)
⇒ \(\widehat{B_1}=\widehat{C_1}\) (hai góc tương ứng)
*Ta có: \(\left\{{}\begin{matrix}KB=AB-AK\\HC=AC-AH\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}AB=AC\left(gt\right)\\AK=AH\left(gt\right)\end{matrix}\right.\)
⇒ KB = HC
*Xét ΔOBK và ΔOCH có:
\(\left\{{}\begin{matrix}\widehat{O_1}=\widehat{O_2}\left(\text{đ}\text{ối}.\text{đ}\text{ỉnh}\right)\\KB=HC\left(cmt\right)\\\widehat{B_1}=\widehat{C_1}\left(cmt\right)\end{matrix}\right.\)
⇒ ΔOBK = ΔOCH (g - c - g)
c) *Vì ΔOBK = ΔOCH (cmt)
⇒ OK = OH (hai cạnh tương ứng)
*Xét ΔAOK và ΔAOH có:
\(\left\{{}\begin{matrix}AK=AH\left(gt\right)\\OK=OH\left(cmt\right)\\AO.l\text{à}.c\text{ạnh}.chung\end{matrix}\right.\)
⇒ ΔAOK = ΔAOH (c - c - c)
⇒ \(\widehat{A_1}=\widehat{A_2}\) (hai góc tương ứng)
*Ta có: \(\left\{{}\begin{matrix}\widehat{A_1}=\widehat{A_2}\left(cmt\right)\\AO.n\text{ằm}.gi\text{ữa}.AK.v\text{à}.AH\end{matrix}\right.\)
⇒ AO là tia phân giác của góc A.
d) *Ta có: \(\left\{{}\begin{matrix}\widehat{A_1}=\widehat{A_2}\left(cmt\right)\\AI.n\text{ằm}.gi\text{ữa}.AB.v\text{à}.AC\end{matrix}\right.\)
⇒ AI là tia phân giác của góc A
*Ta có: \(\left\{{}\begin{matrix}AO.l\text{à}.tia.ph\text{â}n.gi\text{ác}.c\text{ủa}.\widehat{A}\left(cmt\right)\\AI.l\text{à}.tia.ph\text{â}n.gi\text{ác}.c\text{ủa}.\widehat{A}\left(cmt\right)\end{matrix}\right.\)
Mà \(\widehat{A}\) chỉ có 1 tia phân giác nên AO và AI trùng nhau.
⇒ A, O, I thẳng hàng.