Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
Lực ma sát Fms = µmg. Vì lực ma sát ngược chiều với chiều chuyển động nên nếu ta chọn chiều (+) theo chiều chuyển động thì lực ma sát ngược chiều dương.
Sau khi hãm phanh chuyển động của xe là chậm dần đều
Áp dụng định luật II Niu-ton:
-Fms = ma
→ a = -µg = 5,88 m/s2
Áp dụng công thức độc lập thời gian có:
v2 – vo2 = 2a
<->02 – 152 = 2.5,88s
→ s = 19,1m

Đáp án A
Lực ma sát F m s = μ m g . Vì lực ma sát ngc chiều với chiều chuyển động nên nếu ta chọn chiều + theo chiều chuyển động thì lực ma sát ngược chiều +
Sau khi hãm phanh chuyển động của xe là chậm dần đều


Hình như thiếu gia tốc rơi tự do
a, Theo định luật II Niuton:
\(\overrightarrow{F_{mst}}+\overrightarrow{N}+\overrightarrow{P}=m\overrightarrow{a}\left(1\right)\)
Chiếu \(\left(1\right)\) lên chiều dương:
\(m.a=-F_{mst}=-\mu.m.g\Rightarrow a=-\dfrac{g}{50}\)
b, Thời gian ô tô tắt máy đến khi dừng lại:
\(t=\dfrac{v-v_0}{a}=\dfrac{750}{g}\left(s\right)\)
c, Quãng đường ô tô đi được cho đến khi dừng lại:
\(s=\dfrac{v^2-v_0^2}{2a}=\dfrac{5625}{g}\left(m\right)\)

\(v_0=36\)km/h=10m/s
\(v=0\)
Gia tốc xe:
\(F_{hl}=m\cdot a=-F_{ms}=-\mu mg\)
\(\Rightarrow a=-\mu\cdot g=-0,05\cdot10=-0,5\)m/s2
Quãng đường vật đi đến khi dừng:
\(v^2-v^2_0=2aS\)
\(\Rightarrow S=\dfrac{v^2-v_0^2}{2a}=\dfrac{0-10^2}{2\cdot\left(-0,5\right)}=100m\)

Gia tốc của ô tô
\(a=\dfrac{v^2-v_0^2}{2s}=\dfrac{\left(15-5\right)^2-15^2}{2\cdot100}=-0,625\left(\dfrac{m}{s^2}\right)\)
Quãng đường ô tô đi đucợ cho đến lúc dừng lại
\(s=\dfrac{v^2-v_0^2}{2a}=\dfrac{0^2-15^2}{2\cdot\left(-0,625\right)}=180\left(m\right)\)

Theo định luật II Niu tơn
\(\overrightarrow{F_{ms}}+\overrightarrow{F_k}+\overrightarrow{N}+\overrightarrow{P}=m\cdot\overrightarrow{a}\)
chiếu theo Oy: \(N=P=mg=5000\cdot10=5\cdot10^4\left(N\right)\)
Chiếu theo Ox:
\(F_k-F_{ms}=m\cdot a\Rightarrow a=\dfrac{F_k-\mu N}{m}=\dfrac{5\cdot10^3-0,04\cdot5\cdot10^4}{5000}=0,6\left(\dfrac{m}{s^2}\right)\)
Vận tốc xe đi được đoạn đường 50 m
\(v=\sqrt{2as+v_0^2}=\sqrt{2\cdot0,6\cdot50+2^2}=8\left(\dfrac{m}{s}\right)\)
Thời gian xe đi được đoạn đường 50 m
\(t=\dfrac{v-v_0}{a}=\dfrac{8-2}{0,6}=10\left(s\right)\)

a. Khi ô tô chuyển động đều, áp dụng định luật II Newton ta có
P → + N → + F k → + F m s → = 0
Chiếu lên trục nằm ngang và trục thẳng đứng ta có:
Fk – Fms = 0 Fk = Fms và
− P + N = 0 ⇒ N = P = m g ⇒ F k = F m s = μ N = μ m g ⇒ μ = F k m g
M à ℘ = F . v ⇒ F k = ℘ v = 20000 10 = 2000 ( N ) ⇒ μ = 2000 4000.10 = 0 , 05
b. Gia tốc chuyển động của ô tô:
a = v t 2 − v 0 2 2 s = 15 2 − 10 2 2.250 = 0 , 25 ( m / s 2 )
Áp dụng định luật II Newton ta có: P → + N → + F k → + F m s → = m a → (5)
Chiếu (5) lên trục nằm ngang và trục thẳng đứng ta tìm được
F k − F m s = m a ; N = P = m g ⇒ F k = m a + μ m g = 4000.0 , 25 + 0 , 05.4000.10 = 3000 ( N )
Công suất tức thời của động cơ ô tô ở cuối quãng đường là:
℘ = Fkvt = 3000.15 = 45000W.
Ta có: v = v 0 + a t ⇒ t = v − v 0 a = 15 − 10 0 , 25 = 20 ( s )
Vận tốc trung bình của ô tô trên quãng đường đó
v ¯ = s t = 250 20 = 12 , 5 ( m / s ) .
Công suất trung bình của động cơ ô tô trên quãng đường đó là:
℘ ¯ = F k . v ¯ = 375000 ( W )

a)Vật chuyển động chậm dần đều.
Gia tốc vật: \(v^2-v_0^2=2aS\)
\(\Rightarrow a=\dfrac{v^2-v_0^2}{2S}=\dfrac{10^2-15^2}{2\cdot126}=-\dfrac{125}{252}\approx-0,5m/s^2\)
b)Thời gian ô tô chạy thêm được 125m kể từ khi hãm phanh.
\(S=v_0t+\dfrac{1}{2}at^2\Rightarrow126=15t+\dfrac{1}{2}\cdot\left(-\dfrac{125}{252}\right)\cdot t^2\)
\(\Rightarrow\left[{}\begin{matrix}t=50,4s\\t=10,08s\end{matrix}\right.\)
c)Thời gian để ô tô dừng lại: \(v=v_0+at\)
\(\Rightarrow0=15+\left(-\dfrac{125}{252}\right)\cdot t\Rightarrow t=30,24s\)
d)Thời gian xe đi thêm 100m là:
\(S'=v_0t+\dfrac{1}{2}at^2\Rightarrow100=15t+\dfrac{1}{2}\cdot\left(-\dfrac{125}{252}\right)\cdot t^2\)
\(\Rightarrow\left[{}\begin{matrix}t=52,85s\\t=7,63s\end{matrix}\right.\)
Vận tốc lúc này: \(v'^2-v_0^2=2aS'\)
\(\Rightarrow v'=\sqrt{2aS+v_0^2}=\sqrt{2\cdot\left(-\dfrac{125}{252}\right)\cdot100+15^2}\approx11,22m/s\)
Chọn trục tọa độ trùng với quỹ đạo chuyển động thẳng của ô tô, chiều dương của trục hướng theo chiều chuyển động. Chọn mốc thời gian là lúc ô tô bắt đầu hãm phanh.
Theo công thức liên hệ giữa quãng đường đi được với vận tốc và gia tốc trong chuyển động thẳng chậm dần đều:
= 2as
Ta suy ra công thức tính gia tốc của ô tô:
Dấu – của gia tốc a chứng tỏ ô tô chuyển động thẳng chậm dần đều có chiều dương đã chọn trên trục tọa độ, tức là ngược chiều với vận tốc ban đầu

Tham khảo
a. v = 54km/h = 15m/s
m = 2 tấn = 2000kg
Lực ma sát:
F\(_{ms}\)=μN=μmg=0,08.2000.10=1600N
Áp dụng định lý biến thiên động năng
12m(v\(^2\)−0)=A\(_F\)+A\(_N\)+A\(_P\)+A\(_{F_{ms}}\)
⇒12.2000.152=AF+0+0−Fms.s=AF−1600.15
⇒A\(_F\)=249000J
Lực động cơ
A\(_F\)=F.s
⇒249000=F.15
⇒F=16600N
b. Thời gian ô tô chuyển động
\(v^2-0^2\)=2as
⇒15\(^2\)=2.a.15
⇒a=7,5(m/\(s^2\))v=at
⇒15=7,5.t
⇒t=2(s)


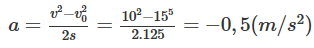
-Fms=m.a
\(\Leftrightarrow-\mu.m.g=m.a\)
\(\Rightarrow a=\)-6m/s2
thời gian xe đi được đến khi dừng lại
t=\(\dfrac{v-v_0}{a}\)=2,5s
quãng đường xe đi được đến khi dừng lại
v2-v02=2as\(\Rightarrow s=\)18,75m