Tập hợp tất cả các giá trị thực của tham số m để hs y= \(\dfrac{-1}{3}x^3+x^2+mx-2019\) nghịch biến trên khoảng (0 ; dương vô cùng)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
1 tháng 12 2017
Chọn D.
![]()
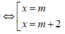
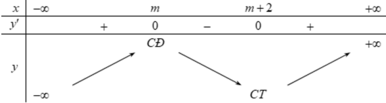
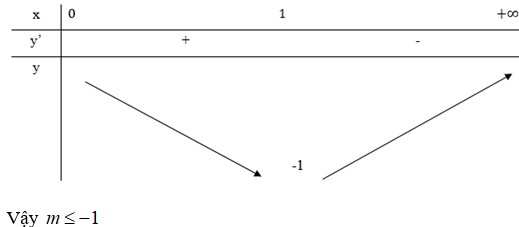
Do đó ta có bảng biến thiên sau:
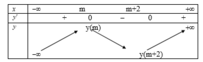
Để hàm số nghịch biến trên khoảng (-1;1) thì
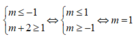

CM
8 tháng 4 2018
Chọn B.
Tập xác định ![]()
Có 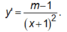
Hàm số nghịch bến trên mỗi khoảng của tập xác định
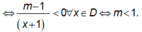

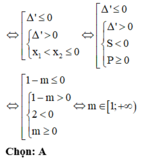
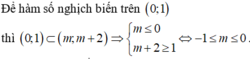

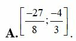
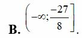

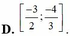


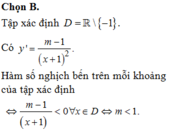
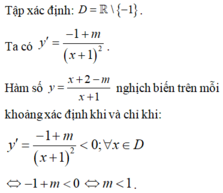

\(f'\left(x\right)=-x^2+2x+m\)
Để hs y = f(x) nghịch biến trên khoảng (0; dương vc)
\(f'\left(x\right)\le0\forall x\in\left(0;+\infty\right)\)
\(-x^2+2x+m\le0\)
\(m\le x^2-2x\)
\(m\le-1\)