ai giúp e với ạ e cảm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



= 23,18 - 3,18 - 4,17 - 5,83 + 51,54 + 8,46
= 20 - 10 + 60
= 70


\(A=\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{x-\sqrt{x}+1}-\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{\sqrt{x}+2}\\ A=\sqrt{x}+1-\sqrt{x}+2=3\)
Anh có thể giải từng bước giúp e ko ạ e ch hỉu lắm í ạ em cảm ơn

\(3,8276< \overline{3,8ab5}< 3,836\)
=>\(276< \overline{ab5}< 360\)
=>\(\left(a,b\right)\in\left\{\left(2;8\right);\left(2;9\right);\left(3;0\right);\left(3;1\right);\left(3;2\right);\left(3;3\right);\left(3;4\right);\left(3;5\right)\right\}\)

Giúp e bài này với ạ không cần làm hết cũng đc ạ ai biết câu nào làm câu đó giúp e nha E cảm ơn nhìu

Em ơi đăng tách bài ra mỗi lượt đăng 1-2 bài thôi nha!


\(26,\\ a,\sin45^0=\cos45^0< \sin50^025'< \sin57^048'=\cos32^012'< \sin72^0=\cos18^0< \sin75^0\\ b,\tan37^026'< \tan47^0< \tan58^0=\cot32^0< \tan63^0< \tan66^019'=\cot23^041'\\ 27,\\ A=\dfrac{\left(\sin^226^0+\sin^264^0\right)+2\left(\cos^215^0+\cos^275^0\right)}{\left(\sin^255^0+\cos^255^0\right)+\left(\sin^242^0+\cos^242^0\right)}-\dfrac{\tan81^0}{2\tan81^0}\\ A=\dfrac{\left(\sin^226^0+\cos^226^0\right)+2\left(\sin^215^0+\cos^215^0\right)}{1+1}-\dfrac{1}{2}\\ A=\dfrac{1+2}{2}-\dfrac{1}{2}=2-\dfrac{1}{2}=\dfrac{3}{2}\)
\(28,\\ \sin^2\alpha=1-\cos^2\alpha=1-\dfrac{1}{2}=\dfrac{1}{2}\\ \Leftrightarrow\sin\alpha=\dfrac{\sqrt{2}}{2}\)
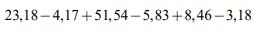


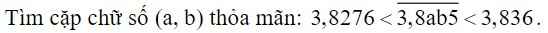



\(\left(\frac{x^2-3x}{x^2-9}-1\right):\left(\frac{9-x^2}{x^2+x-6}-\frac{x-3}{2-x}-\frac{x-2}{x+3}\right)\)
\(=\left(\frac{x^2-3x}{x^2-9}-1\right):\left(\frac{9-x^2}{x^2+x-6}+\frac{x-3}{x-2}-\frac{x-2}{x+3}\right)\)
\(=\left(\frac{x\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}-1\right):\left(\frac{\left(3-x\right)\left(3+x\right)}{x^2+x-6}+\frac{\left(x-3\right)\left(x+3\right)}{\left(x-2\right)\left(x+3\right)}-\frac{\left(x-2\right)^2}{\left(x+3\right)\left(x-2\right)}\right)\)
\(=\left(\frac{x\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}-1\right):\left(\frac{\left(3-x\right)\left(3+x\right)}{x^2+x-6}+\frac{\left(x-3\right)\left(x+3\right)-\left(x-2\right)^2}{x^2+x-6}\right)\)
\(=\left(\frac{x\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}-\frac{\left(x-3\right)\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}\right):\frac{9-x^2+x^2-9-x^2+4x-4}{x^2+x-6}\)
\(=\frac{x\left(x-3\right)-\left(x-3\right)\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}:\frac{-\left(x-2\right)^2}{x^2+x-6}\)
\(=\frac{3\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}:\frac{-\left(x-2\right)^2}{x^2+x-6}\)
\(=\frac{3}{x+3}.\frac{x^2+x-6}{-\left(x-2\right)^2}\)
\(=\frac{3}{x+3}.\frac{\left(x+3\right)\left(x-2\right)}{-\left(x-2\right)^2}\)
\(=\frac{3}{2-x}\)
HT