Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a. \(y'=\dfrac{-1}{\left(x-1\right)}\)
b. \(y'=\dfrac{5}{\left(1-3x\right)^2}\)
c. \(y=\dfrac{\left(x+1\right)^2+1}{x+1}=x+1+\dfrac{1}{x+1}\Rightarrow y'=1-\dfrac{1}{\left(x+1\right)^2}=\dfrac{x^2+2x}{\left(x+1\right)^2}\)
d. \(y'=\dfrac{4x\left(x^2-2x-3\right)-2x^2\left(2x-2\right)}{\left(x^2-2x-3\right)^2}=\dfrac{-4x^2-12x}{\left(x^2-2x-3\right)^2}\)
e. \(y'=1+\dfrac{2}{\left(x-1\right)^2}=\dfrac{x^2-2x+3}{\left(x-1\right)^2}\)
g. \(y'=\dfrac{\left(4x-4\right)\left(2x+1\right)-2\left(2x^2-4x+5\right)}{\left(2x+1\right)^2}=\dfrac{4x^2+4x-14}{\left(2x+1\right)^2}\)
2.
a. \(y'=4\left(x^2+x+1\right)^3.\left(x^2+x+1\right)'=4\left(x^2+x+1\right)^3\left(2x+1\right)\)
b. \(y'=5\left(1-2x^2\right)^4.\left(1-2x^2\right)'=-20x\left(1-2x^2\right)^4\)
c. \(y'=3\left(\dfrac{2x+1}{x-1}\right)^2.\left(\dfrac{2x+1}{x-1}\right)'=3\left(\dfrac{2x+1}{x-1}\right)^2.\left(\dfrac{-3}{\left(x-1\right)^2}\right)=\dfrac{-9\left(2x+1\right)^2}{\left(x-1\right)^4}\)
d. \(y'=\dfrac{2\left(x+1\right)\left(x-1\right)^3-3\left(x-1\right)^2\left(x+1\right)^2}{\left(x-1\right)^6}=\dfrac{-x^2-6x-5}{\left(x-1\right)^4}\)
e. \(y'=-\dfrac{\left[\left(x^2-2x+5\right)^2\right]'}{\left(x^2-2x+5\right)^4}=-\dfrac{2\left(x^2-2x+5\right)\left(2x-2\right)}{\left(x^2-2x+5\right)^4}=-\dfrac{4\left(x-1\right)}{\left(x^2-2x+5\right)^3}\)
f. \(y'=4\left(3-2x^2\right)^3.\left(3-2x^2\right)'=-16x\left(3-2x^2\right)^3\)
Câu 1:
a)
| \(y=f\left(x\right)=2x^2\) | -5 | -3 | 0 | 3 | 5 |
| f(x) | 50 | 18 | 0 | 18 | 50 |
b) Ta có: f(x)=8
\(\Leftrightarrow2x^2=8\)
\(\Leftrightarrow x^2=4\)
hay \(x\in\left\{2;-2\right\}\)
Vậy: Để f(x)=8 thì \(x\in\left\{2;-2\right\}\)
Ta có: \(f\left(x\right)=6-4\sqrt{2}\)
\(\Leftrightarrow2x^2=6-4\sqrt{2}\)
\(\Leftrightarrow x^2=3-2\sqrt{2}\)
\(\Leftrightarrow x=\sqrt{3-2\sqrt{2}}\)
hay \(x=\sqrt{2}-1\)
Vậy: Để \(f\left(x\right)=6-4\sqrt{2}\) thì \(x=\sqrt{2}-1\)
c: Ở hai hàm số trên, nếu lấy biến x cùng một giá trị thì f(x) sẽ nhỏ hơn g(x) 3 đơn vị
a: f(-2)=4+3=7
f(-1)=2+3=5
f(0)=3
f(1/2)=-1+3=2
f(-1/2)=1+3=4
b: g(-1)=1-1=0
f(0)=0-1=-1
1a.
\(y'=3x^2.f'\left(x^3\right)-2x.g'\left(x^2\right)\)
b.
\(y'=\dfrac{3f^2\left(x\right).f'\left(x\right)+3g^2\left(x\right).g'\left(x\right)}{2\sqrt{f^3\left(x\right)+g^3\left(x\right)}}\)
2.
\(f'\left(x\right)=\left(m-1\right)x^3+\left(m-2\right)x^2-2mx+3=0\)
Để ý rằng tổng hệ số của vế trái bằng 1 nên pt luôn có nghiệm \(x=1\), sử dụng lược đồ Hooc-ne ta phân tích được:
\(\Leftrightarrow\left(x-1\right)\left[\left(m-1\right)x^2+\left(2m-3\right)x-3\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\\left(m-1\right)x^2+\left(2m-3\right)x-3=0\left(1\right)\end{matrix}\right.\)
Xét (1), với \(m=1\Rightarrow x=-3\)
- Với \(m\ne1\Rightarrow\Delta=\left(2m-3\right)^2+12\left(m-1\right)=4m^2-3\)
Nếu \(\left|m\right|< \dfrac{\sqrt{3}}{2}\Rightarrow\) (1) vô nghiệm \(\Rightarrow f'\left(x\right)=0\) có đúng 1 nghiệm
Nếu \(\left|m\right|>\dfrac{\sqrt{3}}{2}\Rightarrow\left(1\right)\) có 2 nghiệm \(\Rightarrow f'\left(x\right)=0\) có 3 nghiệm
Giải:
Bài 1: lần lượt thay các giá trị của x, ta có:
_Y=f(-1)= -5.(-1)-1=4
_Y=f(0)= -5.0-1=1
_Y=f(1)= -5.1-1=-6
_Y=f(1/2)= -5.1/2-1=-7/2
Bài 2:
Lần lượt thay các giá trị của x, ta có:
_Y=f(-2)=-2.(-2)+3=7
_Y=f(-1)=-2.(-1)+3=1
_Y=f(0)=-2.0+3=3
_Y=f(-1/2)=-2.(-1/2)+3=4
_Y=f(1/2)=-2.1/2+3=2
a) Thay f(-2) vào hàm số ta có :
y=f(-2)=(-2).(-2)+3=7
Thay f(-1) vào hàm số ta có :
y=f(-1)=(-2).(-1)+3=5
Thay f(0) vào hàm số ta có :
y=f(0)=(-2).0+3=1
Thay f(-1/2) vào hàm số ta có :
y=f(-1/2)=(-2).(-1/2)+3=4
Thay f(1/2) vào hàm số ta có :
y=f(1/2)=(-2).1/2+3=2
b) Thay g(-1) vào hàm số ta có :
y=g(-1)=(-1)2-1=0
Thay g(0) vào hàm số ta có :
y=g(0)=02-1=-1
Thay g(1) vào hàm số ta có :
y=g(1)=12-1=0
Thay g(2) vào hàm số ta có :
y=g(2)=22-1=3
a) \(\left(2x+3y\right)^2=\left(2x\right)^2+2\cdot2x\cdot3y+\left(3y\right)^2=4x^2+12xy+9y^2\)
b) \(\left(x+\dfrac{1}{4}\right)^2=x^2+2\cdot x\cdot\dfrac{1}{4}+\left(\dfrac{1}{4}\right)^2=x^2+\dfrac{1}{2}x+\dfrac{1}{16}\)
c) \(\left(x^2+\dfrac{2}{5}y\right)\left(x^2-\dfrac{2}{5}y\right)=\left(x^2\right)^2-\left(\dfrac{2}{5}y\right)^2=x^4-\dfrac{4}{25}y^2\)
d) \(\left(2x+y^2\right)^3=\left(2x\right)^3+3\cdot\left(2x\right)^2\cdot y^2+3\cdot2x\cdot\left(y^2\right)^2+\left(y^2\right)^3=8x^3+12x^2y^2+6xy^4+y^6\)
e) \(\left(3x^2-2y\right)^2=\left(3x^2\right)^2-2\cdot3x^2\cdot2y+\left(2y\right)^2=9x^4-12x^2y+4y^2\)
f) \(\left(x+4\right)\left(x^2-4x+16\right)=x^3+4^3=x^3+64\)
g) \(\left(x^2-\dfrac{1}{3}\right)\cdot\left(x^4+\dfrac{1}{3}x^2+\dfrac{1}{9}\right)=\left(x^2\right)^3-\left(\dfrac{1}{3}\right)^3=x^6-\dfrac{1}{27}\)
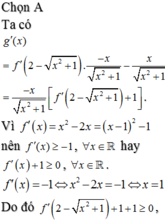
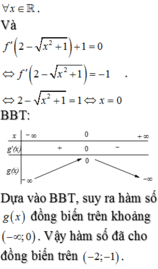
a: \(f\left(x\right)=-\left(x-1\right)^2\)
\(f\left(-\dfrac{1}{3}\right)=-\left(-\dfrac{1}{3}-1\right)^2=-\dfrac{16}{9}\)
\(g\left(-\dfrac{1}{2}\right)=\dfrac{1}{4}-\dfrac{1}{2}+1=\dfrac{1}{4}-\dfrac{2}{4}+\dfrac{4}{4}=\dfrac{3}{4}\)
\(g\left(\dfrac{1}{10}\right)=\dfrac{1}{100}+\dfrac{1}{10}+1=1.01\)
b: Vì \(-\left(x-1\right)^2\le0\forall x\)
nên không có giá trị nào của x để f(x)>0