Một ô tô chuyển động trên s=120km vtb=40km/h biêt nửa thời gian đi dc v1=55km/h tính v=1/2t sau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
\(v_{tb}=\dfrac{AB}{t_1+t_2}\\ \Leftrightarrow45=\dfrac{135}{\dfrac{AB}{2.v_1}+\dfrac{AB}{2.v_2}}\\ \Leftrightarrow45=\dfrac{135}{\dfrac{135}{2.50}+\dfrac{135}{2.v_2}}\\ \Leftrightarrow45=\dfrac{135}{1,35+\dfrac{67,5}{v_2}}\\ \Leftrightarrow1,35+\dfrac{67,5}{v_2}=\dfrac{135}{45}=3\\ \Leftrightarrow\dfrac{67,5}{v_2}=1,65\\ \Leftrightarrow v_2=\dfrac{67,5}{1,65}\approx41\left(km/h\right)\)
Công thức mà áp dụng thôi bạn
\(v_{tb}=\dfrac{AB}{t_1+t_2}=\dfrac{AB}{\dfrac{S_1}{v_1}+\dfrac{S_2}{v_2}}=\dfrac{AB}{\dfrac{AB}{2v_1}+\dfrac{AB}{2v_2}}\)
\(\Leftrightarrow v_{tb}=\dfrac{1}{\dfrac{1}{2v_1}+\dfrac{1}{2v_2}}\Leftrightarrow45=\dfrac{1}{\dfrac{1}{2.50}+\dfrac{1}{2.v_2}}\Rightarrow v_2=...\left(km/h\right)\)

1/ gọi t1 là thời gian ô tô chạy 1/3 quãng đường đầu
=> t1 = s / ( 3 * v1 ) = s / 120
gọi t2 là thời gian ô tô chạy 1/3 quãng đường tiếp theo
=> t2 = s / ( 3 * v2 ) = s / 150
gọi t3 là thời gian ô tô chạy 1/3 quãng đường cuối cùng
=> t3 = s / ( 3 * v3 )
ta có v tb = s / t = s / ( s / 120 + s / 150 + s / ( 3 *v3) )
=> 45 = s / [s ( 1/ 120 + 1/ 150 + 1/ ( 3 *v3 ) ) ]
=> 45 = 1 / ( 3 / 200 + 1 / ( 3 * v3 )
=> 1 / 45 = 3 / 200 + 1/ ( 3 * v3 )
=> 1 / ( 3 *v3 ) = 1 / 45 - 3 / 200
=> 1 / ( 3 *v3 ) = 13 / 1800
=> 3 * v3 = 1800 / 13
=> v3 = 1800 / 39 = khoảng 46,15 km / h
2/Tính vận tốc trung bình của xe đi từ A đến B
vtb = s/t
theo bài ra ta có : s/2 = 20*t1 và s/2 = 60*t2
=> vtb = s/( t1 + t2) = s/ ( s/40 + s/ 120 ) = 30 (km/h)
Tính vận tốc trung bình của xe đi từ B đến A
theo bài ra ta cũng có
t/2 = s1/20 và t/2 = s2/60
=> vtb" = (s1 + s2 )/t = ( 10t + 30t )/t = 40 ( km/h)
Mà nếu xe từ B xuất phát muộn hơn so với xe xuất phát từ A 30phút = 1/2 h thì 2 xe đến địa điểm cùng 1 lúc
=> sA-B = 30*t
sB-A = 40 * ( t - 1/2)
Mà sA-B = sB-A => 30*t = 40 * ( t - 1/2) => t= 2 (h)
Vậy s = 60 ( km)

Gọi x(km) là quãng đường AB (x<0,x \(\in\) Z)
Thời gian ô tô đi :\(\dfrac{x}{40}\)
Thời gian về ô tô chạy: \(\dfrac{x}{55}\)
Thời gian về ít hơn thời gian đi là nửa giờ = \(\dfrac{1}{2}\)
Ta có pt:
\(\dfrac{x}{55}\) - \(\dfrac{x}{40}\) = \(\dfrac{1}{2}\)
\(\dfrac{-3}{440}\) x =\(\dfrac{1}{2}\)
x = \(\dfrac{220}{3}\)
Vậy quãng đường AB là:\(\dfrac{220}{3}\)
con số hơi xấu nha=))

Ok bro, tóm gọn lại:
Đề bài:
- 1/3 quãng đường: đi với \(v_{1} = 45\) km/h
- 2/3 còn lại:
- 2/3 thời gian với \(v_{2} = 55\) km/h
- 1/3 thời gian với \(v_{3} = ?\)
- Vận tốc trung bình: \(v_{t b} = 48\) km/h
Giải nhanh:
Gọi quãng đường \(S\), tổng thời gian:
- \(t_{1} = \frac{S}{135}\)
- \(t_{2} = \frac{29 S}{2160}\)
Tính quãng đường đoạn 2 theo \(v_{2}\), \(v_{3}\):
\(\frac{2}{3} S = \left(\right. \frac{110 + v_{3}}{3} \left.\right) \cdot \frac{29 S}{2160}\)
Rút gọn:
\(\left(\right. 110 + v_{3} \left.\right) \cdot \frac{29}{2160} = \frac{2}{3} \Rightarrow 110 + v_{3} = \frac{4320}{29} \approx 148.97 \Rightarrow v_{3} \approx 39 \&\text{nbsp};\text{km}/\text{h}\)
✅ Đáp số:
\(\boxed{v_{3} \approx 39 \&\text{nbsp};\text{km}/\text{h}}\)
@ VŨ HẢI TÂN, bạn chép mạng đúng không? Bạn vui lòng ghi thêm chữ "tham khảo" ở phần đầu bài nhé!

Ta có thời gian xe ô tô đi trên nữa quãng đường thứ nhất:
\(t_1=\dfrac{s_1}{v_1}=\dfrac{\dfrac{s_{AB}}{2}}{120}=\dfrac{s_{AB}}{240}\left(h\right)\)
Thời gian xe ô tô đi trên nữa quãng đường còn lại:
\(t_2=\dfrac{s_2}{v_2}=\dfrac{\dfrac{s_{AB}}{4}}{80}=\dfrac{s_{AB}}{320}\left(h\right)\)
Thời gian xe ô tô đi trên quãng đường còn lại:
\(t_3=\dfrac{s_3}{v_3}=\dfrac{\dfrac{s_{AB}}{4}}{40}=\dfrac{s_{AB}}{160}\left(h\right)\)
Vận tốc trung bình của xe ô tô là:
\(v_{tb}=\dfrac{s_1+s_2+s_3}{t_1+t_2+t_3}=\dfrac{s_{AB}}{\dfrac{s_{AB}}{240}+\dfrac{s_{AB}}{320}+\dfrac{s_{AB}}{160}}\approx74\left(km/h\right)\)

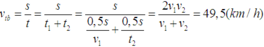

Áp dụng công thức tính vận tốc trung bình ta có:
\(v_{tb}=\dfrac{S}{t_1+t_2}\)
=> \(t_1+t_2\)= \(\dfrac{S}{v_{tb}}\)=\(\dfrac{120}{40}\)= 3 (h)
Ta có: \(t_1+t_2\)= 3 (h)
=>\(\dfrac{S}{v_1}+\dfrac{S}{v_2}=3\left(h\right)\)
=>\(\dfrac{120}{55}+\dfrac{120}{v_2}=3\left(h\right)\)
=> \(\dfrac{120}{v_2}=\dfrac{9}{11}\)(h)
=> \(v_2=\dfrac{120}{\dfrac{9}{11}}\)=\(\dfrac{440}{3}\)(km/h)
Vậy vận tốc của nửa thời gian sau là \(\dfrac{440}{3}\)(km/h)
Sai rồi bạn ơi