Bài 3 câu,C 🙏
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt \(\sqrt{\dfrac{x^2}{x-3}}=a\left(a>=0\right)\)
Theo đề, ta có bất phương trình:
\(a^2>2a+8\)
=>(a-4)(a+2)>0
=>a-4>0
\(\Leftrightarrow\dfrac{x^2}{x-3}>16\)
\(\Leftrightarrow x^2-16x+48>0\)
\(\Leftrightarrow x\in R\)
Vậy: S=R\{3}


15:
b: Gọi I(a;b)
Theo đề, ta có: d(I;d)=d(I;d')=căn 5
=>3a-b+3=căn 5*căn 10=5*căn 2 và a-3b+9=5căn 2
=>|3a-b+3|=|a-3b+9|
=>2a+2b=6 và 2a-4b=12
=>a=1 và b=2
=>I(1;2)
Phương trình (C) là:
(x-1)^2+(y-2)^2=5
c: (C): x^2+y^2+4x-y+4=0
=>(x+2)^2+(y-1/2)^2=1/4
=>I(-2;1/2);R=1/2
=>I'(2;1/2)
Phương trình (C') là:
(x-2)^2+(y-1/2)^2=1/4

a, \(\left(-17\right)+5+8+17+\left(-3\right)\)
\(=\left(-17+17\right)+\left[5+\left(-3\right)\right]+8\)
\(=0+8+8=8+8=16\)
b, \(\left(5^{19}:5^{17}+3\right):7=\left(5^2+3\right):7\)
\(=\left(25+3\right):7=28:7=4\)
c, \(|-8|+\left(-5\right)+9+\left(-7\right)+|-4|\)
\(=8-5+9-7+4=3+2+4=5+4=9\)
ý d mk ko biết nha.
thông cảm cho mk nha.
k mk nha.
#mon

3.
Xét \(x^2-8x+7\le0\Leftrightarrow\left(x-1\right)\left(x-7\right)\le0\Rightarrow1\le x\le7\)
Có tập nghiệm \(D_1=\left[1;7\right]\)
Xét \(x^2-\left(2m+1\right)x+m^2+m\le0\Leftrightarrow\left(x-m\right)\left(x-m-1\right)\le0\)
\(\Leftrightarrow m\le x\le m+1\) có tập nghiệm là \(D_2=\left[m;m+1\right]\)
a. Hệ BPT vô nghiệm khi \(D_1\cap D_2=\varnothing\)
\(\Leftrightarrow\left[{}\begin{matrix}m>7\\m+1< 1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m>7\\m< 0\end{matrix}\right.\)
b. Do \(D_2\) là đoạn có độ dài bằng \(m+1-m=1\) nên hệ có tập nghiệm là 1 đoạn dài 1 trên trục số khi: \(D_2\subset D_1\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ge1\\m+1\le7\end{matrix}\right.\) \(\Rightarrow1\le m\le6\)

Bài 3:
Gọi 4 số chẵn lt là \(a,a+2,a+4,a+6\left(a\in N\right)\)
Ta có \(\dfrac{a+a+2+a+4+a+6}{4}=2007\)
\(\Rightarrow a\times4+12=2007\times4=8028\\ \Rightarrow a\times4=8016\\ \Rightarrow a=2004\)
Vậy 4 số cần tìm là 2004,2006,2008,2010

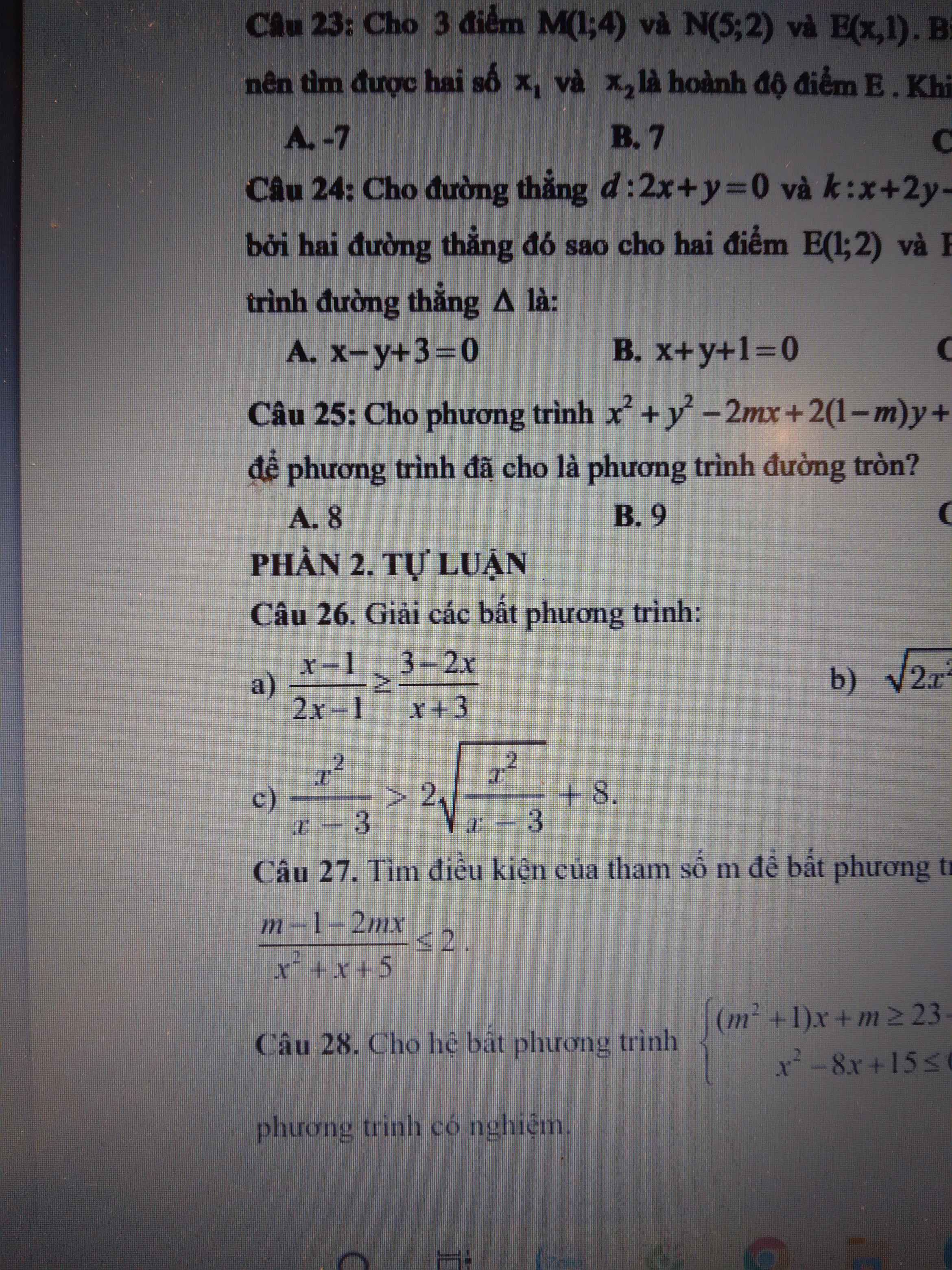






 giải giúp mình bài 3 với nhé 🙏🙏🙏
giải giúp mình bài 3 với nhé 🙏🙏🙏
c: Ta có: \(\sqrt{25x-50}+2\cdot\sqrt{\dfrac{49x-98}{4}}=6\)
\(\Leftrightarrow5\sqrt{x-2}+7\sqrt{x-2}=6\)
\(\Leftrightarrow12\sqrt{x-2}=6\)
\(\Leftrightarrow x-2=\dfrac{1}{4}\)
hay \(x=\dfrac{9}{4}\)