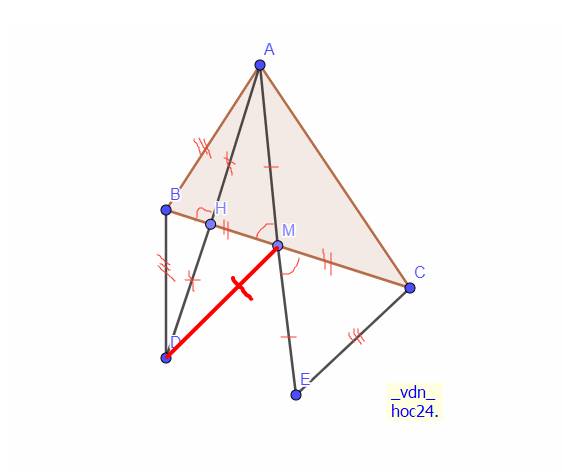
Cho tam giác ABC (AB < AC) , AH vuông góc BC tại H. Trên tia đối của tia HA lấy điểm D sao cho HD = HA, gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA.
a) Chứng minh : AB = CE và BD = CE.
b) Gọi F là trung điểm của DE. Chứng minh MF vuông góc với DE.
c) MF có song song với AD không? Vì sao?


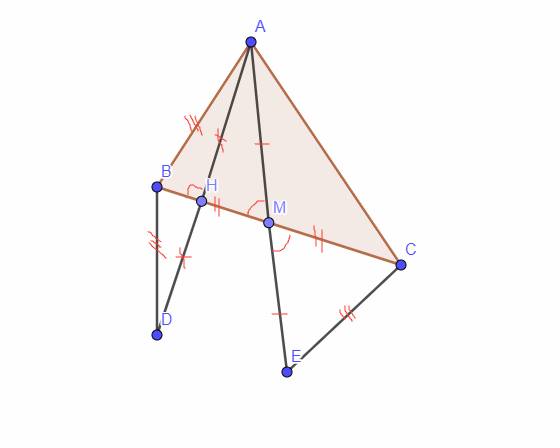
a: Xét tứ giác ABEC có
M là trung điểm của AE
M là trung điểm của BC
Do đó: ABEC là hình bình hành
Suy ra: AB=CE(1)
Xét ΔABD có
BH là đường cao
BH là đường trung tuyến
Do đó: ΔABD cân tại B
=>BA=BD(2)
Từ (1) và (2) suy ra BD=CE
b: Xét ΔADE có
H là trung điểm của AD
M là trung điểm của AE
Do đó: HM là đường trung bình
=>HM//DE
hay DE\(\perp\)AD
Ta có: ΔADE vuông tại D
mà DM là đường trung tuyến
nên DM=ME
=>ΔMED cân tại M
mà MF là đường trung tuyến
nên MF là đường cao
c: MF\(\perp\)DE
AD\(\perp\)DE
Do đó: MF//AD