vẽ hình hộ nữa nha
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) - Trong hình vẽ có tất cả 12 góc
b) - Có 6 cặp góc đối đỉnh ( không kể góc bẹt)
O x x' y y' z z'

a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
b: Xét ΔAHD vuông tại H và ΔAKE vuông tại K có
AD=AE
\(\widehat{HAD}=\widehat{KAE}\)
Do đó: ΔAHD=ΔAKE
Suy ra: HD=EK
c: Xét ΔABC có
AH/AB=AK/AC
nên HK//BC

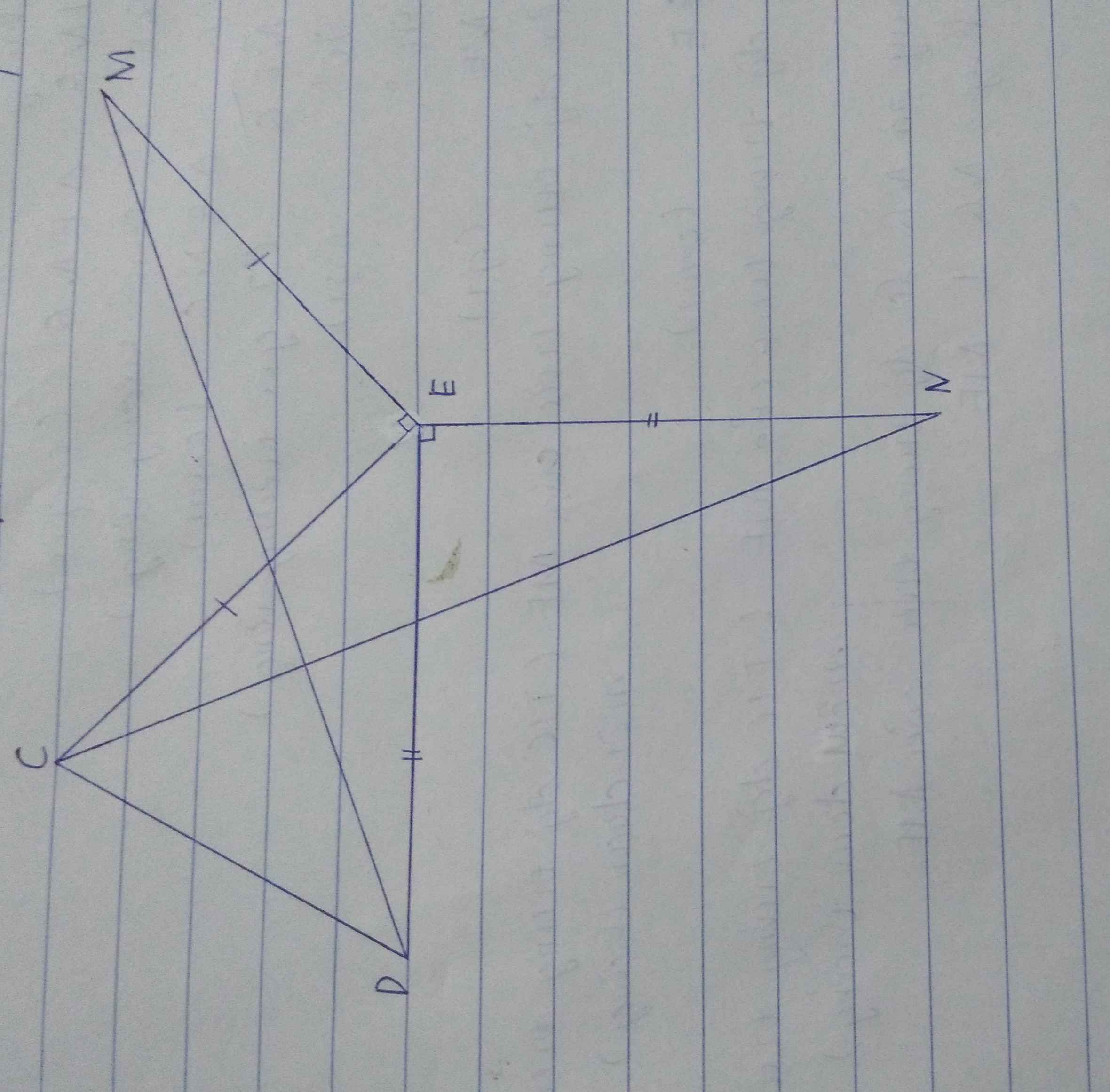
a) Dễ dàng c/m đc tam giác MED = tam giác CEN
=> MD = CN (2 cạnh tương ứng)
b) Gọi O là giao điểm của CE và DM
Tam giác MED = tam giác CEN
=> Góc EMD = Góc ECN (2 góc tương ứng)
Mà: \(\left\{{}\begin{matrix}\widehat{EOM}=\widehat{COD}\left(đối-đỉnh\right)\\\widehat{EOM}+\widehat{EMD}=90^0\end{matrix}\right.\)
=> Góc ECN + Góc COD = 90o
=> Góc COM = 90o
=> MD vuông góc CN
a) Ta chứng minh đc tam giác MED = tam giác CEN
=> MD = CN (2 cạnh tương ứng)
b) Gọi O là giao điểm của CE và DM
Tam giác MED = tam giác CEN
=> Góc EMD = Góc ECN (2 góc tương ứng)
Mà: {ˆEOM=ˆCOD(đối−đỉnh)ˆEOM+ˆEMD=900{EOM^=COD^(đối−đỉnh)EOM^+EMD^=900
=> Góc ECN + Góc COD = 90o
=> Góc COM = 90o
=> MD vuông góc CN

mk ko biết cách vẽ hình trên olm nên bạn thông cảm
Vì d ko cắt BC => đường thẳng d // BC
=> \(\widehat{DAB}=\widehat{BAC},\widehat{DBC}=90^0\)
Xét tam giác ABC có \(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)
=> \(\widehat{ABC}+\widehat{ACB}=90^0\)
=> \(\widehat{ABC}=90^0-\widehat{ACB}\)(1)
Ta lại có \(\widehat{DBC}=90^0\)=> \(\widehat{DAB}+\widehat{ABC}=90^0\)
=> \(\widehat{ABC}=90^0-\widehat{DAB}\)(2)
Từ 1,2 => \(\widehat{ACB}=\widehat{DAB}\)
mà \(\widehat{ABC}=\widehat{ACB}\)( Vì tam giác ABC cân tại A)
=> \(\widehat{DBA}=\widehat{ABC}\)
Mặt khác \(\widehat{DAB}=\widehat{ABC}\)(\(d//BC\))
=> \(\widehat{DAB}=\widehat{DBA}\)
=> tam giác DAB cân tại D => DA=DB
Tương tự : AE=EC
=> BD + CE =AD+AE
=> BD+CE = DE (đpcm)
Ta có d đi qua A, D và E thuộc d
=>D, A, E thẳng hàng =>^DAB+^BAC+^CAE=180° =>^DAB+^CAE=90°(1)
Xét tam giác DAB vuông ở D =>^DBA+^DAB=90°(2)
Từ (1) và (2) =>^CAE=^DAB
Xét tam giác BAD và tam giác ACE có: ^DAB=^CAE(cmt)
AB=AC(tam giác ABC cân) ^ADB=^AEC(=90°)
=>Tam giác BAD tam giác ACE(g.c.g)
=> BD=AE; EC=AD
Mà DE=AD+AE
=>DE=BD+CE

a: OA<OB
=>A nằm giữa O và B
=>OA+AB=OB
=>AB=2cm
b: Vì OA<OC
nên A nằm giữa O và C
mà OA=1/2OC
nên A là trung điểm của OC

a: Xét (O) có
\(\widehat{EBF}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{EBF}=90^0\)
Xét (O) có
\(\widehat{EAF}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{EAF}=90^0\)
Xét ΔDEF có
EB là đường cao ứng với cạnh FD
FA là đường cao ứng với cạnh DE
EB cắt FA tại H
Do đó: H là trực tâm của ΔDEF
b: Xét tứ giác DAHB có
\(\widehat{DAH}+\widehat{DBH}=180^0\)
nên DAHB là tứ giác nội tiếp
hay D,A,H,B cùng thuộc 1 đường tròn
c: Ta có: I là tâm của đường tròn ngoại tiếp tứ giác DAHB
Suy ra: IA=IB
hay I nằm trên đường trung trực của AB(1)
Ta có: O là tâm đường tròn ngoại tiếp tứ giác ABFE
Suy ra: OA=OB
hay O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OI là đường trung trực của AB
hay OI\(\perp\)AB
d: Điểm K ở đâu vậy bạn?

Xét tứ giác MAOB có
\(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)
=>MAOB là tứ giác nội tiếp
=>M,A,O,B cùng thuộc một đường tròn
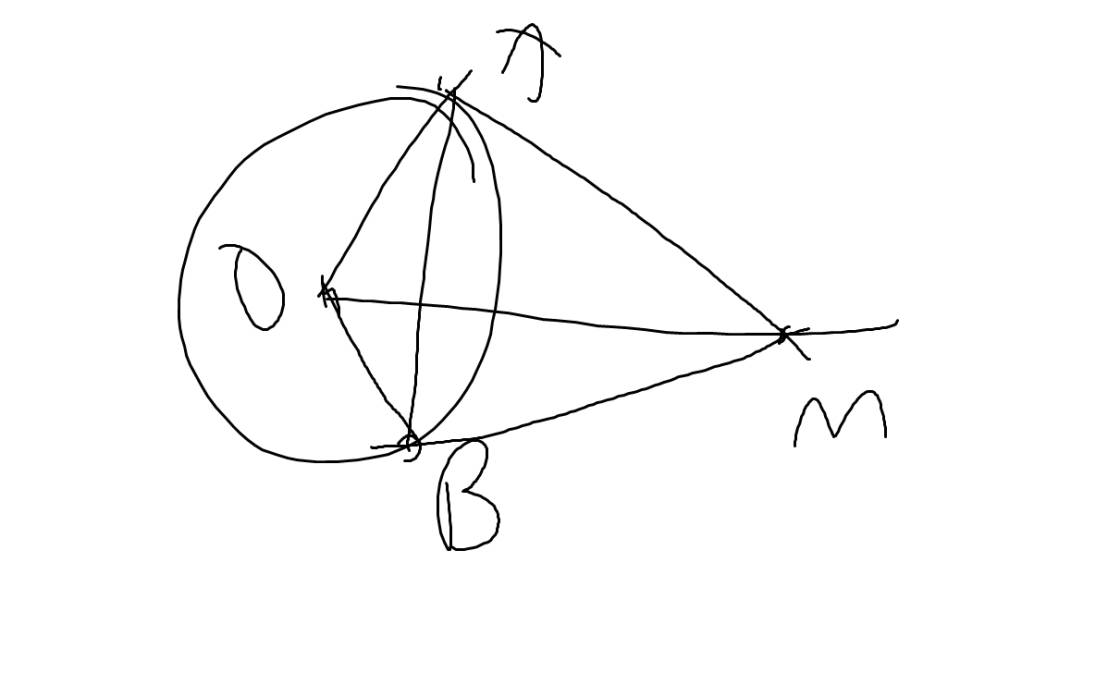
 Vẽ hộ mình cả hình nữa với! Mình cảm ơn nhiều
Vẽ hộ mình cả hình nữa với! Mình cảm ơn nhiều