tìm GTNN
h(x)= \(\dfrac{x^2-x+1}{\left(x-1\right)^2}\)
k(x)=\(\dfrac{5x^2-22x+25}{x^2-4x+4}\)
help me![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(P=sin^22x-\left[2sin\dfrac{x}{2}cos\dfrac{x}{2}\left(cos^4\dfrac{x}{2}-sin^4\dfrac{x}{2}\right)\right]^2\)
\(=sin^22x-\left[sinx\left(cos^2\dfrac{x}{2}-sin^2\dfrac{x}{2}\right)\left(cos^2\dfrac{x}{2}+sin^2\dfrac{x}{2}\right)\right]^2\)
\(=sin^22x-\left[sinx.cosx.1\right]^2\)
\(=sin^22x-\left[\dfrac{1}{2}sin2x\right]^2\)
\(=\dfrac{3}{4}sin^22x=\dfrac{3}{4}\left(1-cos^22x\right)=\dfrac{3}{4}\left(1-\dfrac{1}{4}\right)=\dfrac{9}{16}\)

\(\dfrac{x}{x-1}-\dfrac{2x}{x^2-1}=0\left(ĐKXĐ:x\ne\pm1\right)\\ \Leftrightarrow\dfrac{x\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}-\dfrac{2x}{\left(x-1\right)\left(x+1\right)}=0\\ \Rightarrow x^2+x-2x=0\\ \Leftrightarrow x^2-x=0\Leftrightarrow x\left(x-1\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=0\\x-1=0\Rightarrow x=1\left(loại\right)\end{matrix}\right.\)
vậy phương trình có tập nghiệm là S={0}.
b)
\(\dfrac{\left(x+2\right)^2}{2x-3}-1=\dfrac{x^2+10}{2x-3}\left(ĐKXĐ:x\ne\dfrac{3}{2}\right)\)
quy đồng và khử mẫu phương trình trên, ta được:
\(\left(x+2\right)^2+3-2x=x^2+10\\ \Leftrightarrow x^2+4x+4-2x-x^2=10-3\)
\(\Leftrightarrow2x+4=7\Leftrightarrow2x=7-4=3\Rightarrow x=\dfrac{3}{2}\left(loại\right)\)
vậy phương trình đã cho vô nghiệm.
c)\(\dfrac{x+5}{x-5}-\dfrac{x-5}{x+5}=\dfrac{20}{x^2-25}\left(ĐKXĐ:x\ne\pm5\right)\)
\(\Leftrightarrow\dfrac{\left(x+5\right)^2}{\left(x-5\right)\left(x+5\right)}-\dfrac{\left(x-5\right)^2}{\left(x+5\right)\left(x-5\right)}=\dfrac{20}{\left(x+5\right)\left(x-5\right)}\)
\(\Rightarrow\left(x+5\right)^2-\left(x-5\right)^2=20\)
\(\Leftrightarrow x^2+25x+25-x^2+25x-25=20\\ \Leftrightarrow50x=20\Rightarrow x=\dfrac{2}{5}\)
vậy tập nghiệm của phương trình là \(S=\left\{\dfrac{2}{5}\right\}\)
d)\(\dfrac{3x+2}{3x-2}-\dfrac{6}{2+3x}=\dfrac{9x^2}{9x^2-4}\left(ĐKXĐ:x\ne\pm\dfrac{2}{3}\right)\)
quy đồng và khử mẫu phương trình trên, ta được:
\(\left(3x+2\right)^2-6\left(3x-2\right)=9x^2\\ \Leftrightarrow9x^2+12x+4-18x+12-9x^2=0\\ \Leftrightarrow16-6x=0\Leftrightarrow6x=16\Rightarrow x=\dfrac{16}{6}\)
vậy tập nghiệm của phương trình là \(S=\left\{\dfrac{16}{6}\right\}\)
e)\(\dfrac{3}{5x-1}+\dfrac{2}{3-5x}=\dfrac{4}{\left(1-5x\right)\left(5x-3\right)}\left(ĐKXĐ:x\ne\dfrac{1}{5};\dfrac{3}{5}\right)\)
quy đồng và khử mẫu phương trình trên, ta được:
\(3\left(3-5x\right)+2\left(5x-1\right)=4\\ \Leftrightarrow9-15x+10x-2=4\\ \Leftrightarrow-5x=-3\Rightarrow x=\dfrac{3}{5}\left(loại\right)\)
vậy phương trình đã cho vô nghiệm.
f)
\(\dfrac{3}{1-4x}=\dfrac{2}{4x+1}-\dfrac{8+6x}{16x^2-1}\left(ĐKXĐ:x\ne\pm\dfrac{1}{4}\right)\)
quy đồng và khử mẫu phương trình trên, ta được:
\(-3\left(4x+1\right)=2\left(4x-1\right)-8-6x\\ \Leftrightarrow-12x-3=8x-2-8-6x\\ \Leftrightarrow-14x=-7\Rightarrow x=\dfrac{1}{2}\)
vậy phương trình có tập nghiệm là \(S=\left\{\dfrac{1}{2}\right\}\)
g)
\(\dfrac{y-1}{y-2}-\dfrac{5}{y+2}=\dfrac{12}{y^2-4}+1\left(ĐKXĐ:y\ne\pm2\right)\)
quy đồng và khử mẫu phương trình trên, ta được:
\(\left(y-1\right)\left(y+2\right)-5\left(y-2\right)=12+y^2-4\\ \Leftrightarrow y^2+y-2-5y+10=12+y^2-4\\ \Leftrightarrow-4y+8=8\Leftrightarrow-4y=0\Rightarrow y=0\)
vậy phương trình có tập nghiệm là S={0}
h)
\(\dfrac{x+1}{x-1}-\dfrac{x-1}{x+1}=\dfrac{4}{x^2-1}\left(ĐKXĐ:x\ne\pm1\right)\)
quy đồng và khử mẫu phương trình trên, ta được:
\(\left(x+1\right)^2-\left(x-1\right)^2=4\\ \Leftrightarrow x^2+2x+1-x^2+2x-1=4\\ \Leftrightarrow4x=4\Rightarrow x=1\)
vậy phương trình có tập nghiệm là S={1}.
i)
\(\dfrac{2x-3}{x+2}-\dfrac{x+2}{x-2}=\dfrac{2}{x^2-4}\left(ĐKXĐ:x\ne\pm2\right)\)
quy đồng và khử mẫu phương trình trên, ta được:
\(\left(2x-3\right)\left(x-2\right)-\left(x+2\right)=2\\ \Leftrightarrow2x^2-7x+6-x^2-4x-4=2\\ \Leftrightarrow x^2-11x=0\Rightarrow\left[{}\begin{matrix}x=0\\x-11=0\Rightarrow x=11\end{matrix}\right.\)
vậy phương trình có tập nghiệm là S={0;11}
j)
\(\dfrac{x-1}{x^2-4}=\dfrac{3}{2-x}\left(ĐKXĐ:x\ne\pm2\right)\)
quy đồng và khử mẫu phương trình trên, ta được:
\(x-1=-3\left(x+2\right)\Leftrightarrow x-1=-3x-6\\ \Leftrightarrow4x=5\Rightarrow x=\dfrac{5}{4}\)
vậy phương trình có tập nghiệm là \(S=\left\{\dfrac{5}{4}\right\}\)

\(y=x+\dfrac{1}{x}-5\ge2\sqrt{\dfrac{x}{x}}-5=-3\)
\(y_{min}=-3\) khi \(x=1\)
\(y=4x^2+\dfrac{1}{2x}+\dfrac{1}{2x}-4\ge3\sqrt[3]{\dfrac{4x^2}{2x.2x}}-4=-1\)
\(y_{min}=-1\) khi \(x=\dfrac{1}{2}\)
\(y=x+\dfrac{4}{x}\Rightarrow y'=1-\dfrac{4}{x^2}=0\Rightarrow x=-2\)
\(y\left(-2\right)=-4\Rightarrow\max\limits_{x>0}y=-4\) khi \(x=-2\)

Lời giải:
Ta có:
\(C=\frac{5(x^2-4x+4)-2x+5}{x^2-4x+4}=\frac{5(x-2)^2-2(x-2)+1}{(x-2)^2}=5-\frac{2}{x-2}+\frac{1}{(x-2)^2}\)
Đặt $\frac{1}{x-2}=t$ thì:
$C=t^2-2t+5=(t-1)^2+4\geq 4$ với mọi $t$
$\Rightarrow C_{\min}=4$. Vậy GTNN của $C$ là $4$. Giá trị này đạt tại $t=1$
$\Leftrightarrow \frac{1}{x-2}=1\Leftrightarrow x=3$

Bài 1:
\(B=\dfrac{4\left(x+3\right)^2}{\left(3x+5\right)^2-4x^2}-\dfrac{\left(x^2-25\right)}{9x^2-\left(2x+5\right)^2}-\dfrac{\left(2x+3\right)^2-x^2}{\left(4x+15\right)^2-x^2}\)
\(=\dfrac{4\left(x+3\right)^2}{\left(3x+5-2x\right)\left(3x+5+2x\right)}-\dfrac{\left(x-5\right)\left(x+5\right)}{\left(3x-2x-5\right)\left(3x+2x+5\right)}-\dfrac{\left(2x+3-x\right)\left(2x+3+x\right)}{\left(4x+15-x\right)\left(4x+15+x\right)}\)
\(=\dfrac{4\left(x+3\right)^2}{5\left(x+5\right)\left(x+1\right)}-\dfrac{\left(x-5\right)\left(x+5\right)}{5\left(x-5\right)\left(x+1\right)}-\dfrac{3\left(x+3\right)\left(x+1\right)}{15\left(x+5\right)\left(x+3\right)}\)
\(=\dfrac{4\left(x+3\right)^2}{5\left(x+5\right)\left(x+1\right)}-\dfrac{x+5}{5\left(x+1\right)}-\dfrac{x+1}{5\left(x+5\right)}\)
\(=\dfrac{4\left(x+3\right)^2}{5\left(x+5\right)\left(x+1\right)}-\dfrac{\left(x+5\right)^2}{5\left(x+5\right)\left(x+1\right)}-\dfrac{\left(x+1\right)^2}{5\left(x+5\right)\left(x+1\right)}\)
\(=\dfrac{4\left(x^2+6x+9\right)-\left(x^2+10x+25\right)-\left(x^2+2x+1\right)}{5\left(x+5\right)\left(x+1\right)}\)
\(=\dfrac{4x^2+24x+36-x^2-10x-25-x^2-2x-1}{5\left(x+5\right)\left(x+1\right)}\)
\(=\dfrac{2x^2+12x+10}{5\left(x+5\right)\left(x+1\right)}\)
\(=\dfrac{2\left(x^2+6x+5\right)}{5\left(x+5\right)\left(x+1\right)}\)
\(=\dfrac{2\left(x^2+5x+x+5\right)}{5\left(x+5\right)\left(x+1\right)}\)
\(=\dfrac{2\left(x+5\right)\left(x+1\right)}{5\left(x+5\right)\left(x+1\right)}=\dfrac{2}{5}\)
đc bn , nhg mà đề bài câu a b2 sao tự nhiên lại có " n "
bn xem lại đề đi

\(a,=\dfrac{\left(x-2\right)^2-\left(x+2\right)^2}{\left(x-2\right)^2\left(x+2\right)^2}:\dfrac{x-2+x+2}{\left(x-2\right)\left(x+2\right)}\\ =\dfrac{-8x}{\left(x-2\right)^2\left(x+2\right)^2}\cdot\dfrac{\left(x-2\right)\left(x+2\right)}{2x}=\dfrac{-4}{\left(x-2\right)\left(x+2\right)}\)
\(b,=\dfrac{5x^2+26xy+5y^2+5x^2-26xy+5y^2}{x\left(x-5y\right)\left(x+5y\right)}\cdot\dfrac{\left(x-5y\right)\left(x+5y\right)}{x^2+y^2}\\ =\dfrac{10\left(x^2+y^2\right)}{x\left(x^2+y^2\right)}=\dfrac{10}{x}\)

1.
\(G=\dfrac{2}{x^2+8}\le\dfrac{2}{8}=\dfrac{1}{4}\)
\(G_{max}=\dfrac{1}{4}\) khi \(x=0\)
\(H=\dfrac{-3}{x^2-5x+1}\) biểu thức này ko có min max
2.
\(D=\dfrac{2x^2-16x+41}{x^2-8x+22}=\dfrac{2\left(x^2-8x+22\right)-3}{x^2-8x+22}=2-\dfrac{3}{\left(x-4\right)^2+6}\ge2-\dfrac{3}{6}=\dfrac{3}{2}\)
\(D_{min}=\dfrac{3}{2}\) khi \(x=4\)
\(E=\dfrac{4x^4-x^2-1}{\left(x^2+1\right)^2}=\dfrac{-\left(x^4+2x^2+1\right)+5x^4+x^2}{\left(x^2+1\right)^2}=-1+\dfrac{5x^4+x^2}{\left(x^2+1\right)^2}\ge-1\)
\(E_{min}=-1\) khi \(x=0\)
\(G=\dfrac{3\left(x^2-4x+5\right)-5}{x^2-4x+5}=3-\dfrac{5}{\left(x-2\right)^2+1}\ge3-\dfrac{5}{1}=-2\)
\(G_{min}=-2\) khi \(x=2\)

a: ĐKXĐ: x<>1; x<>2; x<>3
\(K=\left(\dfrac{x^2}{\left(x-2\right)\left(x-3\right)}+\dfrac{x^2}{\left(x-1\right)\left(x-2\right)}\right)\cdot\dfrac{\left(x-1\right)\left(x-3\right)}{x^4+2x^2+1-x^2}\)
\(=\dfrac{x^3-x^2+x^3-3x^2}{\left(x-2\right)\left(x-3\right)\left(x-1\right)}\cdot\dfrac{\left(x-1\right)\left(x-3\right)}{\left(x^2+1+x\right)\left(x^2+1-x\right)}\)
\(=\dfrac{2x^3-4x^2}{\left(x-2\right)}\cdot\dfrac{1}{\left(x^2+x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{2x^2\left(x-2\right)}{\left(x-2\right)\left(x^4+x^2+1\right)}=\dfrac{2x^2}{x^4+x^2+1}\)
b:
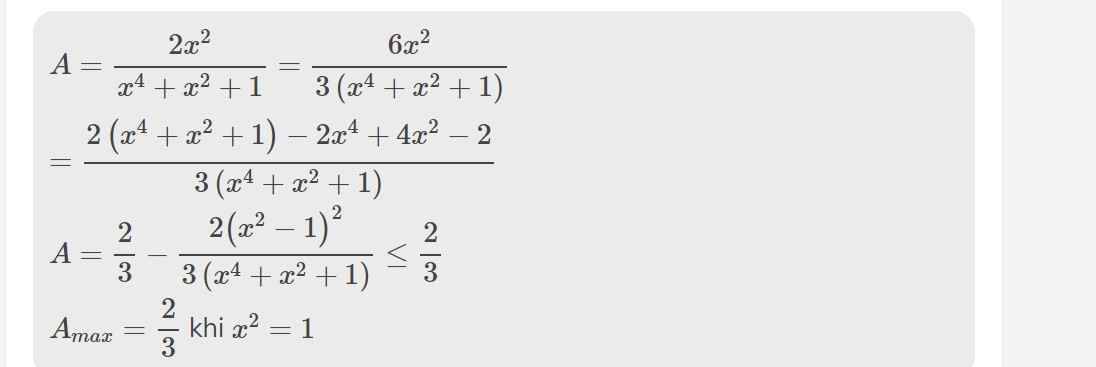
\(k\left(x\right)=\dfrac{5x^2-22x+25}{x^2-4x+4}\)
\(\Leftrightarrow k\left(x\right)=\dfrac{5x^2-20x+20-x+2-x+2+1}{x^2-4x+4}\)
\(\Leftrightarrow k\left(x\right)=\dfrac{\left(5x^2-20x+20\right)-\left(x-2\right)-\left(x-2\right)+1}{x^2-4x+4}\)
\(\Leftrightarrow k\left(x\right)=\dfrac{5\left(x^2-4x+4\right)-\left(x-2\right)-\left(x-2\right)+1}{x^2-4x+4}\)
\(\Leftrightarrow k\left(x\right)=\dfrac{5\left(x-2\right)^2-\left(x-2\right)-\left(x-2\right)+1}{\left(x-2\right)^2}\)
\(\Leftrightarrow k\left(x\right)=\dfrac{5\left(x-2\right)^2}{\left(x-2\right)^2}-\dfrac{x-2}{\left(x-2\right)^2}-\dfrac{x-2}{\left(x-2\right)^2}+\dfrac{1}{\left(x-2\right)^2}\)
\(\Leftrightarrow k\left(x\right)=5-\dfrac{1}{x-2}-\dfrac{1}{x-2}+\dfrac{1}{\left(x-2\right)^2}\)
Đặt \(y=\dfrac{1}{x-2}\)
\(\Rightarrow k\left(x\right)=5-y-y+y^2=y^2-2y+1+4=\left(y-1\right)^2+4\ge4\)
Vậy GTNN của \(k\left(x\right)=4\) khi \(y=1\Rightarrow\dfrac{1}{x-2}=1\Leftrightarrow x=3\)
\(h\left(x\right)=\dfrac{x^2-x+1}{\left(x-1\right)^2}\)
\(\Leftrightarrow h\left(x\right)=\dfrac{x^2-2x+1+x-1+1}{\left(x-1\right)^2}\)
\(\Leftrightarrow h\left(x\right)=\dfrac{\left(x-1\right)^2}{\left(x-1\right)^2}+\dfrac{x-1}{\left(x-1\right)^2}+\dfrac{1}{\left(x-1\right)^2}\)
\(\Leftrightarrow h\left(x\right)=1+\dfrac{1}{x-1}+\dfrac{1}{\left(x-1\right)^2}\)
Đặt \(y=\dfrac{1}{x-1}\)
\(\Rightarrow h\left(x\right)=1+y+y^2\)
\(\Rightarrow h\left(x\right)=y^2+y+1\)
\(\Rightarrow h\left(x\right)=y^2+2.y.\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(\Rightarrow h\left(x\right)=\left(y+\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)
=> GTNN của \(h\left(x\right)=\dfrac{3}{4}\) khi \(y+\dfrac{1}{2}=0\Leftrightarrow y=\dfrac{-1}{2}\)
\(\Leftrightarrow\dfrac{1}{x-1}=\dfrac{-1}{2}\)
\(\Leftrightarrow x=-1\)