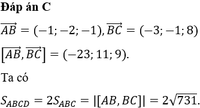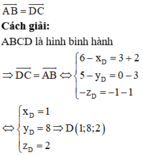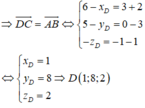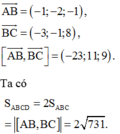1. Cho hình bình hành ABCD với A(1;3), D(5;2) cạnh BC đi qua điểm M(3/2;-1). biết tâm của hbh nằm trên trục hoành. Tìm tọa độ điểm C.
2. Trong mp(Oxy). Cho 3 điểm A (1;0), B(0;3), C (-3;-5)
a) Xác định tọa độ điểm I thỏa mãn hệ thức: \(2\overrightarrow{IA}\) - \(3\overrightarrow{IB}\) + \(2\overrightarrow{IC}\) = \(\overrightarrow{0}\)
b) Giả sử N(-4;1). Tìm tọa độ giao điểm I của hai đg chéo tứ giác AONB.