cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau;
a)Gọi E,F,G,H tương ứng là trung điểm các cạnh AB,BC,CD,DA.Chứng minh rằng EFGH là hình chữ nhật
b) Gọi I,J,K,L tương ứng là trung điểm các cạnh EF,FG,GH,HE nói ở câu a). Chứng minh rằng IJHL là hình thoi
c)Gọi M,N,P,Q tương ứng là trung điểm các cạnh IJ,JK,KL,LI nói ở câu b).Chứng minh rằng MNPQ là hình vuông
d) Khi AC vuông góc với BD và AC=BD thì ccas tứ giác EFGH, IJKL,MNPQ

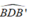 = 90° ( góc nội tiếp chắn nửa đường tròn)
= 90° ( góc nội tiếp chắn nửa đường tròn)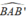 = 90° ( góc nội tiếp chắn nửa đường tròn)
= 90° ( góc nội tiếp chắn nửa đường tròn)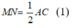
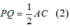
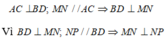
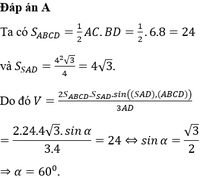
a) Tam giác ABC có
AE=EB(gt)
BF=FC(gt)
Suy ra EF là đường trung bình cua tâm giác anh
Suy ra EF=AC/2 và EF//AC(1)
Tương tự chứng minh HG là đường trung bình của tam giác ADC
Suy ra HG//AC và HG=AC(2)
Từ 1 và 2
Suy ra EF=HG và EF//HG
Suy ra EFGH là hình bình hành
Tam giác ABD có
AE=ED(gt)
EH=HD(gt)
Suy ra EH là đường trung bình
Suy ra EH//BD
Mà BD vuông góc AC(gt)
Suy ra EH vuông góc AC
Mà EF//AC(cmt)
Suy ra EF vuông góc EH
Suy ra góc HEF = 90 độ
Mà EFGH là hình bình hành(cmt)
Suy ra ÈGH là hình chữ nhật
b)Trễ rồi nên ghi ý nhà
B1)Chứng minh LI là đường trung bình của tam giác HEF
B2)Chúng mình JK là đường trung bình của tâm giác FGH
B3)Chứng minh IJKL là hình bình hành mà BD vuông góc AC, suy ra ỊKL là hình thoi