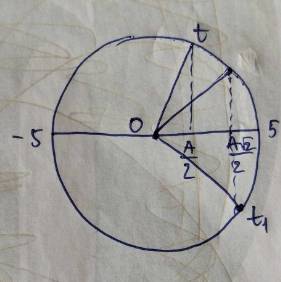
một vật thực hiện đồng thời 2 dao động điều hòa cùng phương, cùng tần số có phương trình x1=\(\sqrt{3}cos\left(20\pi t-\frac{\pi}{2}\right)\left(cm\right)\)và x2=\(cos\left(20\pi t\right)\left(cm\right)\) xác định thời điểm đầu tiên vật đi qua li độ x=-1cm theo chiều dương. giúp mình với nhé...!! thanks