cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau;
a)Gọi E,F,G,H tương ứng là trung điểm các cạnh AB,BC,CD,DA.Chứng minh rằng EFGH là hình chữ nhật
b) Gọi I,J,K,L tương ứng là trung điểm các cạnh EF,FG,GH,HE nói ở câu a). Chứng minh rằng IJHL là hình thoi
c)Gọi M,N,P,Q tương ứng là trung điểm các cạnh IJ,JK,KL,LI nói ở câu b).Chứng minh rằng MNPQ là hình vuông
d) Khi AC vuông góc với BD và AC=BD thì ccas tứ giác EFGH, IJKL,MNPQ

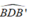 = 90° ( góc nội tiếp chắn nửa đường tròn)
= 90° ( góc nội tiếp chắn nửa đường tròn)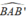 = 90° ( góc nội tiếp chắn nửa đường tròn)
= 90° ( góc nội tiếp chắn nửa đường tròn)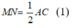
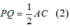
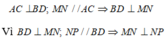
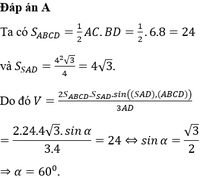
a) Xét \(\bigtriangleup\)BAC, có: E là trung điểm BA
F là trung điểm BC
=> EF là đường trung bình của \(\bigtriangleup\)BAC
=> EF//AC và EF=\(\dfrac{1}{2}\)AC (1)
Xét\(\bigtriangleup\)DAC, có: H là trung điểm AD
G là trung điểm DC
=> HG là đường trung bình của \(\bigtriangleup\)DAC
=> HG//AC và HG=\(\dfrac{1}{2}\)AC (2)
Từ (1)và (2) => HG//EF và HG=EF
=> EFGH là hình bình hành.(3)
Xét\(\bigtriangleup\)CBD, có: F là trung điểm CB
G là trung điểm CD
=> FG là đường trung bình của \(\bigtriangleup\)CBD
=> FG// BD
Có: EF//AC
FG//BD
Mà AC \(\bot\)BD => EF \(\bot\)FG(4)
Từ (3) và (4)=> EFGH là hình chữ nhật.
ạn biết vẽ hình ko vẽ giúp luôn với ạ