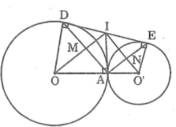
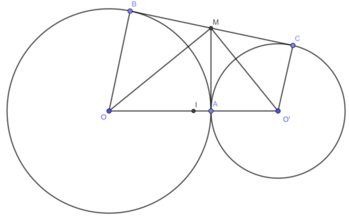
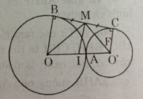
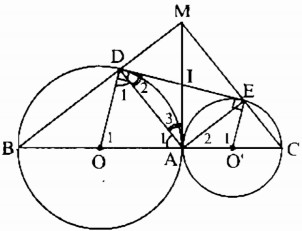
cho 2 đường tròn (o) và (o') tiếp xúc ngoài tại a ,kẻ đường kính ad của (o) và đường kính ae của (o') . tiếp tuyến chung ngoài bc của (o) và (o') [b thuộc (o)và c thuộc (o')] gọi i là giao điểm của bd và ce
a) tính góc bac
b) tứ giác abic là hình gì ?
c) CMR: ai là tiếp tuyến của 2 đg tròn
d) CMR: ib.id=ic.ie
e) CMR: bde + bce =180