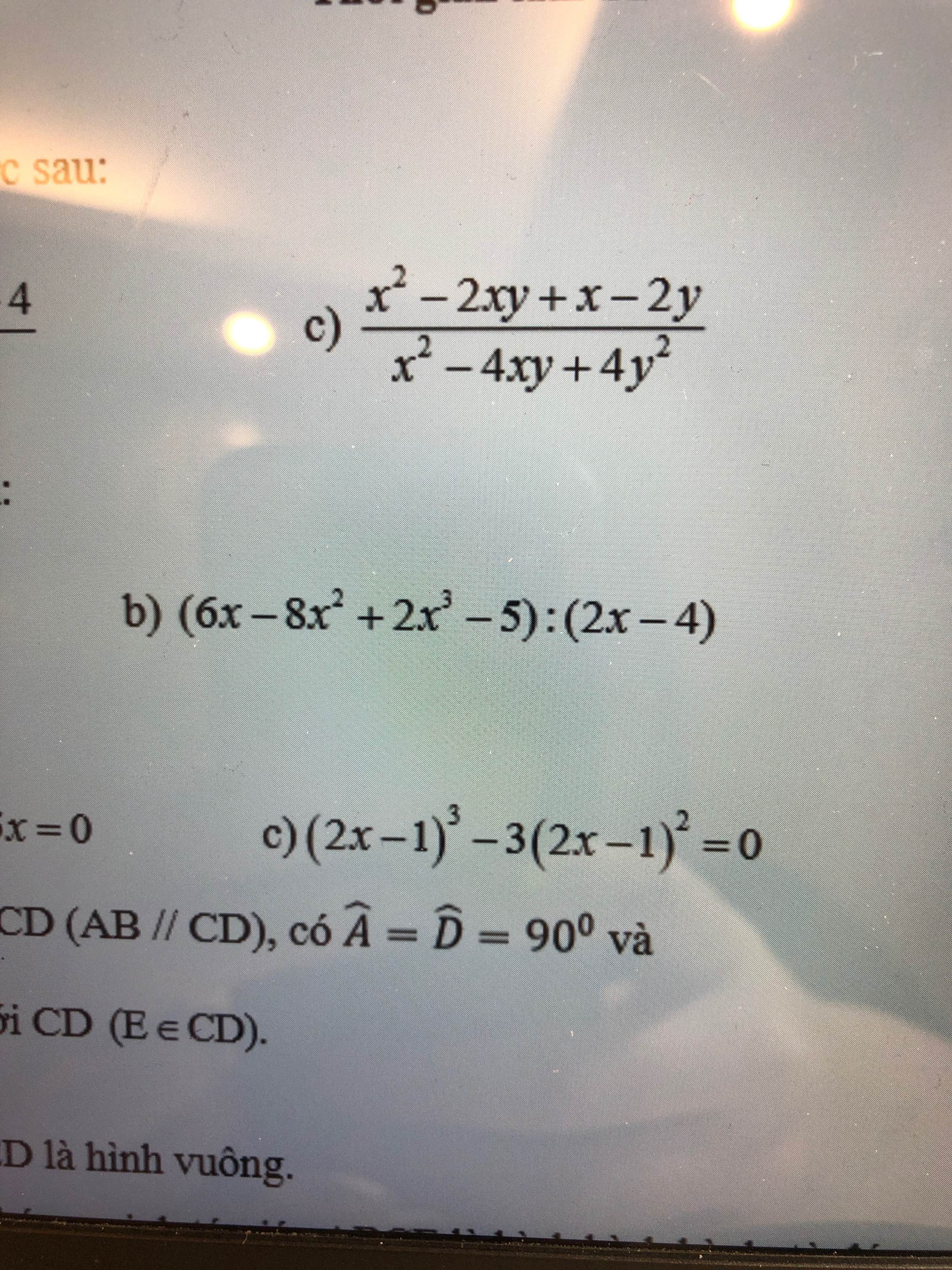Giải hộ mình câu d với câu f. Cảm ơn mn nhiều
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
S
Shauna
30 tháng 8 2021
Đúng(1)
Những câu hỏi liên quan
31 tháng 8 2021
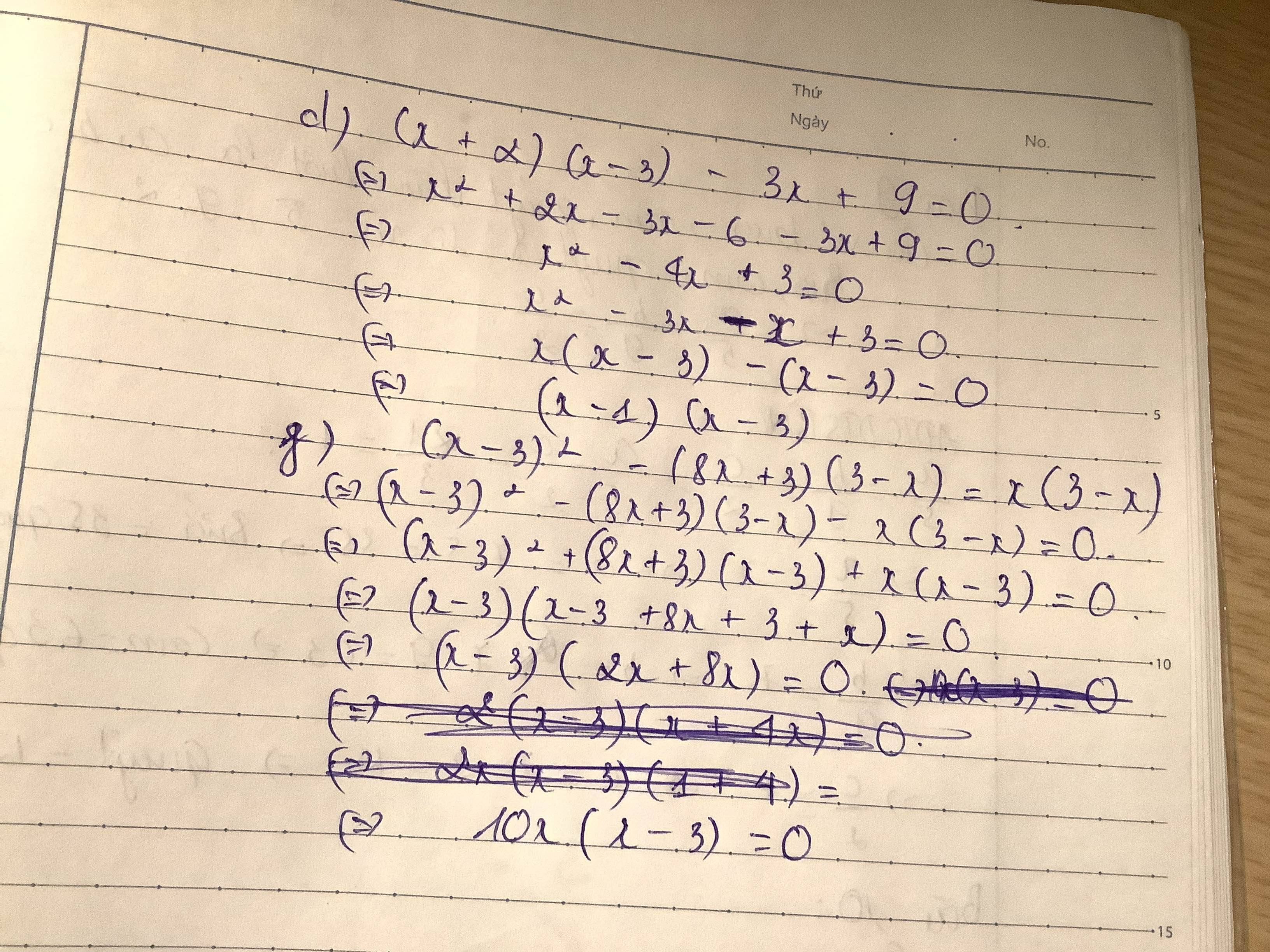
bài 7
\(x^{n+2}-x^n\)
\(=x^{n+2-n}=x^2\)
\(\left(b\right)x^{x+3}-x^{x+1}=x^{x+3-x-1}=X^2\)
c)
\(x^{2m}+x^m=x^{2m+m}=x^{2m}\)
d)
\(x^{2n+1}-x^{4n}=x^{2n+1-4n}=x^{1-2n}\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
12 tháng 8 2023
\(\dfrac{12}{16}=\dfrac{132}{176}\\ \dfrac{13}{16}=\dfrac{143}{176}\\ Ta.có:\dfrac{16}{22}< \dfrac{132}{176}< \dfrac{17}{22}< \dfrac{143}{176}< \dfrac{18}{22}\\ Vậy:Chọn.số.17\)
18 tháng 2 2021
1) Vì x=25 thỏa mãn ĐKXĐ nên Thay x=25 vào biểu thức \(A=\dfrac{\sqrt{x}-2}{x+1}\), ta được:
\(A=\dfrac{\sqrt{25}-2}{25+1}=\dfrac{5-2}{25+1}=\dfrac{3}{26}\)
Vậy: Khi x=25 thì \(A=\dfrac{3}{26}\)
2) Ta có: \(B=\dfrac{\sqrt{x}-3}{\sqrt{x}+1}+\dfrac{2x+8\sqrt{x}-6}{x-\sqrt{x}-2}\)
\(=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-5\sqrt{x}+6+2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3x+3\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}}{\sqrt{x}-2}\)
S
Mn ơi, giải hộ mik câu này với! Tối nay mik phải nộp rồi ạ! Cảm ơn mn nhiều lắm!
2
NN
1
24 tháng 11 2021
\(2b,=\left(2x^3-4x^2-4x^2+8x-2x+4-9\right):\left(2x-4\right)\\ =\left[\left(2x-4\right)\left(x^2-2x-2\right)-9\right]:\left(2x-4\right)\\ =x^2-2x-2\left(\text{ dư -9}\right)\)
KV
14 tháng 12 2023
a) \(\left(x+2\right)^2=4\left(2x-1\right)^2\)
\(\left(x+2\right)^2-4\left(2x-1\right)^2=0\)
\(\left(x+2\right)^2-\left[2\left(2x-1\right)\right]^2=0\)
\(\left(x+2\right)^2-\left(4x-2\right)^2=0\)
\(\left(x+2-4x+2\right)\left(x+2+4x-2\right)=0\)
\(6x\left(-3x+4\right)=0\)
\(\Rightarrow6x=0\) hoặc \(-3x+4=0\)
*) \(6x=0\)
\(x=0\)
*) \(-3x+4=0\)
\(3x=4\)
\(x=\dfrac{4}{3}\)
Vậy \(x=0;x=\dfrac{4}{3}\)
b) \(4x\left(x-2019\right)-x+2019=0\)
\(4x\left(x-2019\right)-\left(x-2019\right)=0\)
\(\left(x-2019\right)\left(4x-1\right)=0\)
\(\Rightarrow x-2019=0\) hoặc \(4x-1=0\)
*) \(x-2019=0\)
\(x=2019\)
*) \(4x-1=0\)
\(4x=1\)
\(x=\dfrac{1}{4}\)
Vậy \(x=\dfrac{1}{4};x=2019\)
31 tháng 10 2021
\(PT\Leftrightarrow\sqrt{\left(x^2+1\right)^3}-1+3x^4-4x^3=0\\ \Leftrightarrow\dfrac{\left(x^2+1\right)^3-1}{\sqrt{\left(x^2+1\right)^3}+1}+x^2\left(3x^2-4x\right)=0\\ \Leftrightarrow x^2\left[\dfrac{\left(x^2+1\right)^2+\left(x^2+1\right)+1}{\sqrt{\left(x^2+1\right)^3}+1}+3x^2-4x\right]=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\\dfrac{2+x^2+\left(x^2+1\right)^2}{\sqrt{\left(x^2+1\right)^3}+1}+3x^2-4x=0\left(1\right)\end{matrix}\right.\\ \left(1\right)\ge\dfrac{2+0+1}{1+1}+3x^2-4x=3x^2-4x+\dfrac{3}{2}>0\)
Vậy PT có nghiệm \(x=0\)