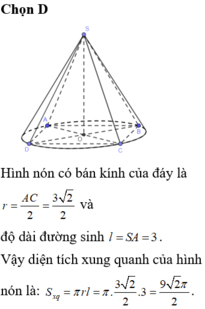
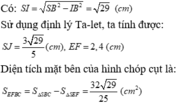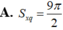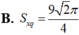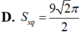cho em hỏi cách tính chiều cao của hình chóp nón cụt ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HB
13 tháng 5 2017
\(a,S_{xp}=4.\dfrac{a+2a}{2}.a=6a^2\)
\(b,\)Vẽ một mặt bên. Ta có:\(AH=\dfrac{AB-A^'B^'}{2}=\dfrac{2a-a}{2}=\dfrac{a}{2}\)
Trong tamn giác vuông A'HA:
\(AA^'=\sqrt{a^2+\left(\dfrac{a}{2}\right)^2}=\sqrt{\dfrac{5a^2}{4}}\)
Từ đó tính tiếp sẽ ra chiều cao hình chóp
Đáp số :Độ dài cạnh bên là :\(\sqrt{\dfrac{5a^2}{4}}\)
Chiều cao chóp cụt :\(\sqrt{\dfrac{3a^2}{4}}\)
CM
14 tháng 12 2019
Kẻ A'H ⊥ AB.
Ta có K là trung điểm của AB, I là trung điểm của A'B'. O và O' là tâm của hai hình vuông đáy.
Ta có: A'I =a/2 ; AK = a ⇒ AH =a/2
Áp dụng định lí Pi-ta-go vào tam giác vuông AA'H, ta có:
A ' A 2 = A ' H 2 + A H 2 = a 2 + a 2 / 4 = 5 a 2 / 4
Suy ra: AA' = 5 a 2 / 4
Kẻ IE ⊥ OK, ta có: OK = a ⇒ EK = a/2
Áp dụng định lí Pi-ta-go vào tam giác vuông IEK, ta có:
I K 2 = I E 2 + E K 2
Suy ra: I E 2 = I K 2 - E K 2 = a 2 - a / 2 2 = 3 a 2 / 4
Vậy IE = 3 a 2 / 4
CM
29 tháng 3 2018
Một mặt bên của hình chóp cụt là một hình thang có hai đáy là a và 2a; đường cao bằng a.
Diện tích mặt bên là:
S = (a+ 2a): 2.a =3/2 a 2 (đvtt)
Diện tích xung quanh hình nón cụt:
S x q = 4.3/2 a 2 = 6 a 2 (đvtt)
CM
25 tháng 6 2019
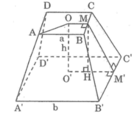
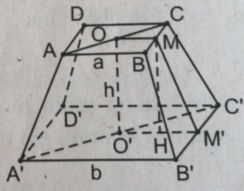
Xét hình chóp cụt đều ABCD.A'B'C'D' như hình bs.19.
Gọi M, M' thứ tự là trung điểm của BC, B'C'. Khi đó MM' là đường cao của hình thang cân BCC'B'.
Do đó diện tích xung quanh của hình chóp cụt đều là:
S x q = 4.(a+b)/2.MM′=(2a+2b).MM′
Từ giả thiết ta có:
(2a+2b).MM′=
a
2
+
b
2
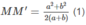
Dễ thấy OM // O'M' nên OM và O'M' xác định mặt phẳng (OMM'O'). Trong mặt phẳng (OMM'O'), kẻ MH ⊥ O'M'. Khi đó: HM' = O'M' – O'H = (b−a)/2
Trong tam giác vuông MHM' ta có: M M ' 2 = M H 2 + H M ' 2 = h + b - a / 2 2 (2)
Từ (1) và (2) suy ra :
10 tháng 5 2017
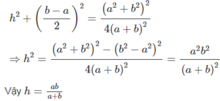
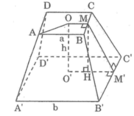
Xét hình chóp cụt đều ABCD.AB'C'D'
Gọi M ,M' thứ tự là trung điểm của BC , B'C' . Khi đó MM' là đường cao của hình thang cân BCC'B' . Do đó diện tích xung quanh của hình chóp cụt đều là :
\(S_{xq}=4.\dfrac{a+b}{2}.MM'=\left(2a+2b\right).MM'\)
Từ giả thiết , ta có :
\(\left(2a+2b\right).MM'=a^2+b^2hayMM'=\dfrac{a^2+b^2}{2\left(a+b\right)}\left(1\right)\)
Dễ thấy OM // O'M' nên OM và O'M' xác định mặt phẳng (OMM'O') . Trong mặt phẳng (OMM'O') , kẻ MH \(\perp\) O'M' . Khi đó : \(HM'=O'M'-O'H=\dfrac{b-a}{2}\)
Trong tam giác vuông MHM' ta có :
\(MM'^2=MH^2+HM'^2=h^2+\left(\dfrac{b-a}{2}\right)^2\left(2\right)\)
Từ (1) và (2) suy ra :
\(h^2+\left(\dfrac{b-a}{2}\right)^2=\dfrac{\left(a^2+b^2\right)^2}{4\left(a+b\right)^2}\)
\(\Rightarrow h^2=\dfrac{\left(a^2+b^2\right)^2-\left(b^2-a^2\right)^2}{4\left(a+b\right)^2}=\dfrac{a^2b^2}{\left(a+b\right)^2}\)
Vậy \(h=\dfrac{ab}{a+b}\)
CM
3 tháng 3 2019
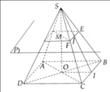
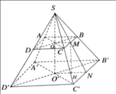
a) Gọi O là tâm của đáy ABCD, M là giao điểm của SO và mặt phẳng (P). Ta có: OM = 2(cm).
Ta tính được O B = 2 2 c m rồi suy ra SO = 5 (cm)
Từ đó chiều cao cần tìm là: SM = SO - OM 3 (cm)
b) Gọi I là trung điểm của BC. E, F, J lần lượt là giao điểm của SB, SC, SI với mặt phẳng (p).
