Tính diện tích hình bình hành ABCD biết \(\widehat{A}\)= \(\alpha\)<\(90^o\), AB = a, AD = d
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 8
ABCD là hình bình hành
=>AB=CD
=>CD=6(cm)
Diện tích tam giác ADC là:
\(S_{ADC}=\frac12\cdot DA\cdot DC\cdot\sin ADC=\frac12\cdot4\cdot6\cdot\sin60=2\cdot6\cdot\frac{\sqrt3}{2}=6\sqrt3\left(\operatorname{cm}^2\right)\)
ABCD là hình bình hành
=>\(S_{ABCD}=2\cdot S_{ADC}=2\cdot6\sqrt3=12\sqrt3\left(\operatorname{cm}^2\right)\)
Ta có: \(\hat{KAB}+\hat{BAD}=180^0\) (hai góc kề bù)
\(\hat{BAD}+\hat{ADC}=180^0\) (ABCD là hình bình hành)
Do đó: \(\hat{KAB}=\hat{ADC}=60^0\)
Xét ΔKAB vuông tại K có \(\sin KAB=\frac{KB}{AB}\)
=>\(\frac{KB}{6}=\sin60=\frac{\sqrt3}{2}\)
=>\(KB=6\cdot\frac{\sqrt3}{2}=3\sqrt3\left(\operatorname{cm}\right)\)
ΔKAB vuông tại K
=>\(KA^2+KB^2=AB^2\)
=>\(KA^2=6^2-\left(3\sqrt3\right)^2=36-27=9=3^2\)
=>KA=3(cm)
Diện tích tam giác KAB là:
\(S_{KAB}=\frac12\cdot KA\cdot KB=\frac12\cdot3\cdot3\sqrt3=\frac{9\sqrt3}{2}\left(\operatorname{cm}^2\right)\)
Ta có: BC//AD
=>\(\hat{HCB}=\hat{ADC}\) (hai góc đồng vị)
=>\(\hat{HCB}=60^0\)
Xét ΔHBC vuông tại H có \(\sin HCB=\frac{HB}{BC}\)
=>\(\frac{HB}{4}=\sin60=\frac{\sqrt3}{2}\)
=>\(HB=4\cdot\frac{\sqrt3}{2}=2\sqrt3\left(\operatorname{cm}\right)\)
ΔBHC vuông tại H
=>\(HB^2+HC^2=BC^2\)
=>\(HC^2=4^2-\left(2\sqrt3\right)^2=16-12=4=2^2\)
=>HC=2(cm)
ΔBHC vuông tại H
=>\(S_{HBC}=\frac12\cdot HB\cdot HC=\frac12\cdot2\cdot2\sqrt3=2\sqrt3\left(\operatorname{cm}^2\right)\)
Diện tích tứ giác KBHD là:
\(S_{KBHD}=S_{ABCD}+S_{BAK}+S_{BCH}\)
\(=12\sqrt3+\frac{9\sqrt3}{2}+2\sqrt3=14\sqrt3+4,5\sqrt3=18,5\sqrt3\left(\operatorname{cm}^2\right)\)
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
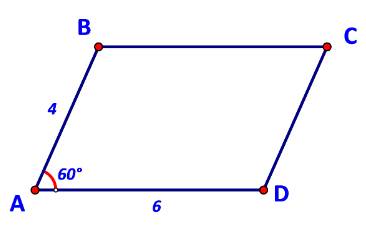
a) \(\overrightarrow {BD} = \overrightarrow {AD} - \overrightarrow {AB} ;\;\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} .\)
b) \(\overrightarrow {AB} .\overrightarrow {AD} = 4.6.\cos \widehat {BAD} = 24.\cos {60^o} = 12.\)
\(\begin{array}{l}\overrightarrow {AB} .\overrightarrow {AC} = \overrightarrow {AB} (\overrightarrow {AB} + \overrightarrow {AD} ) = {\overrightarrow {AB} ^2} + \overrightarrow {AB} .\overrightarrow {AD} = {4^2} + 12 = 28.\\\overrightarrow {BD} .\overrightarrow {AC} = (\overrightarrow {AD} - \overrightarrow {AB} )(\overrightarrow {AB} + \overrightarrow {AD} ) = {\overrightarrow {AD} ^2} - {\overrightarrow {AB} ^2} = {6^2} - {4^2} = 20.\end{array}\)
c) Áp dụng định lí cosin cho tam giác ABD ta có:
\(\begin{array}{l}\quad \;B{D^2} = A{B^2} + A{D^2} - 2.AB.AD.\cos A\\ \Leftrightarrow B{D^2} = {4^2} + {6^2} - 2.4.6.\cos {60^o} = 28\\ \Leftrightarrow BD = 2\sqrt 7 .\end{array}\)
Áp dụng định lí cosin cho tam giác ABC ta có:
\(\begin{array}{l}\quad \;A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\\ \Leftrightarrow A{C^2} = {4^2} + {6^2} - 2.4.6.\cos {120^o} = 76\\ \Leftrightarrow AC = 2\sqrt {19} .\end{array}\)
NT
1
6 tháng 1 2019
hình bình hành ABCD là hình chữ nhật( vì có 1 góc vuông)
Diện tích hình chữ nhật ABCD là
S= AB *AC= 3*5= 15 cm vuông
CT
0
Có thiếu dữ kiện không vậy
- không thiếu bạn ạ, trong đề bài ghi vậy nên mình cũng ghi vậy luôn .