Giải giúp mình câu d thôi ạ. Xin cảm ơn 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: \(=\dfrac{x+2}{x+2}=1\)
b: \(=\dfrac{2x+6}{x+3}=2\)



b) Để P nguyên thì \(\sqrt{x}+5⋮3\sqrt{x}-1\)
\(\Leftrightarrow3\sqrt{x}+15⋮3\sqrt{x}-1\)
\(\Leftrightarrow16⋮3\sqrt{x}-1\)
\(\Leftrightarrow3\sqrt{x}-1\in\left\{-1;1;2;4;8;16\right\}\)
\(\Leftrightarrow3\sqrt{x}\in\left\{0;2;3;5;9;17\right\}\)
\(\Leftrightarrow3\sqrt{x}\in\left\{0;3;9\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{0;1;3\right\}\)
hay \(x\in\left\{0;1;9\right\}\)

ĐKXĐ : \(x\ne\pm2\)
Ta có : \(A=\left(\dfrac{\left(x+1\right)\left(x+2\right)+x\left(x-2\right)+2x^2+3}{x^2-4}\right):\left(\dfrac{x+2-x+3}{x+2}\right)\)
\(=\left(\dfrac{4x^2+x+5}{x^2-4}\right):\left(\dfrac{5}{x+2}\right)=\dfrac{\left(4x^2+x+5\right)\left(x+2\right)}{5\left(x+2\right)\left(x-2\right)}=\dfrac{4x^2+x+5}{5x-10}\)
\(=\dfrac{4x+9}{5}+\dfrac{23}{5x-10}\)
- Để A nhận giá trị nguyên :
\(5\left(x-2\right)\inƯ_{\left(23\right)}=\left\{1;-1;23;-23\right\}\)
\(\Rightarrow x\in\left\{\dfrac{11}{5};\dfrac{9}{5};\dfrac{33}{5};-\dfrac{13}{5}\right\}\)
=> Không tồn tại x nguyên để A nguyên .
Mọi người giải giúp mình bài này với ạ, cảm ơn mn nhiều, chỉ cần câu c ý chứng minh góc 90 độ thôi ạ

a: Xét tứ giác ABQN có
\(\widehat{BQN}=\widehat{QNA}=\widehat{NAB}=90^0\)
=>ABQN là hình chữ nhật
b: Xét ΔCAD có
DN,CH là các đường cao
DN cắt CH tại M
Do đó: M là trực tâm của ΔCAD
=>AM\(\perp\)CD
c: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\left(=90^0-\widehat{ABC}\right)\)
Do đó: ΔHAB đồng dạng với ΔHCA
=>\(\dfrac{HA}{HC}=\dfrac{HB}{HA}\)
=>\(HA^2=HB\cdot HC\)
=>\(HA=\sqrt{HB\cdot HC}\)

 ai giúp mình giải với mình cần câu c với câu d thôi cũng đc ạ! cảm ơn
ai giúp mình giải với mình cần câu c với câu d thôi cũng đc ạ! cảm ơn 




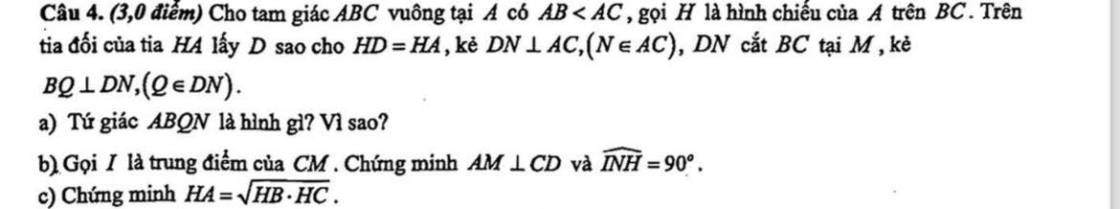
a: Xét ΔABC có
E là trung điểm của AB
F là trung điểm của AC
Do đó: EF là đường trung bình của ΔABC
Suy ra: EF//BC và \(EF=\dfrac{BC}{2}\)
hay \(EF=\dfrac{7.2}{2}=3.6\left(cm\right)\)
b: Xét tứ giác ADCE có
F là trung điểm của đường chéo AC
F là trung điểm của đường chéo ED
Do đó: ADCE là hình bình hành
Suy ra: AE=CD
mà AE=BE
nên CD=BE