Help me bài 2 , 3 . Thanks nhiều nhiều ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NY
1
Những câu hỏi liên quan
NT
1
14 tháng 3 2017
Sai rồi, quan hệ cạnh và góc đối diện không đc áp dụng ở 2 tam giác như bạn làm đâu nhe!
LT
1 tháng 5 2017
a)h(x)=f(x)-g(x)
=(2x3 +3x2 -2x +3)-(2x3 +3x2 -7x +2)
=2x3 + 3x2 - 2x +3 - 2x3 -3x2 + 7x -2
=5x+1
b)h(x)=5x+1=0
=>5x=-1
x=\(\frac{-1}{5}\)
9 tháng 11 2017
Ta có :\(A=3+3^2+3^3+...+3^{2008}\)(1)
\(\Rightarrow3A=3^2+3^3+3^4+...+3^{2009}\)(2)
Lấy (2) trừ đi 1 ta có :
\(\Rightarrow2A=3^{2009}-3\)
Ta lại có :
\(2A+3=3^x\)
\(\Rightarrow3^{2009}=3^x\)
\(\Rightarrow x=2009\)
17 tháng 4 2022
\(\left|2x-3\right|=3-2x\)
\(ĐK:x\le\dfrac{3}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=3-2x\\3-2x=3-2x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\0=0\left(đúng\right)\end{matrix}\right.\)
Vậy \(S=\left\{x\in R;x=\dfrac{3}{2}\right\}\)
QN
28 tháng 4 2017
a) Tìm h(x) = f(x) - g(x)
f(x) - g(x) = (-2x2 - 3x3 - 5x + 5x3 - x + x2 + 4x + 3 + 4x2) - (2x2 - x3 + 3x + 3x3 + x2 - x - 9x + 2)
= -2x2 - 3x3 - 5x + 5x3 - x + x2 + 4x + 3 + 4x2 - 2x2 + x3 - 3x - 3x3 - x2 + x + 9x - 2
= (-2x2 + x2 + 4x2 - 2x2 - x2) + (-3x3 + 5x3 + x3 - 3x3) + (-5x - x + 4x - 3x + x + 9x) + (3 - 2)
= 5x + 1
Vậy h(x) = 5x + 1
b) Tìm nghiệm của đa thức h(x)
Cho h(x) = 0
\(\Leftrightarrow\) 5x + 1 = 0
5x = 0 + 1
5x = 1
x = \(\dfrac{1}{5}\)
Vậy x = \(\dfrac{1}{5}\) là nghiệm của đa thức h(x).
20 tháng 12 2023
e: \(\left(-4156+2021\right)-\left(119+2021-4156\right)\)
\(=-4156+2021-119-2021+4156\)
\(=\left(-4156+4156\right)+\left(2021-2021\right)-119\)
=0+0-119
=-119
g: \(315\cdot75-\left(15\cdot100-315\cdot25\right)\)
\(=315\cdot75-15\cdot100+315\cdot25\)
\(=315\left(75+25\right)-15\cdot100\)
\(=315\cdot100-15\cdot100=300\cdot100=30000\)
h: \(\left(-489\right)\cdot125-\left(125\cdot11-500\cdot25\right)\)
\(=-489\cdot125-125\cdot11+500\cdot25\)
\(=125\left(-489-11\right)+500\cdot25\)
\(=125\cdot\left(-500\right)+500\cdot25\)
\(=500\left(-125+25\right)\)
\(=500\cdot\left(-100\right)=-50000\)
Bài 2:
a: \(-415-3\left(2x-1\right)^2=-490\)
=>\(3\left(2x-1\right)^2+415=490\)
=>\(3\left(2x-1\right)^2=75\)
=>\(\left(2x-1\right)^2=25\)
=>\(\left[{}\begin{matrix}2x-1=5\\2x-1=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=6\\2x=-4\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=3\\x=-2\end{matrix}\right.\)
4 tháng 5 2019
Tôi đây
Ko biết làm bt đó
# USAS - 12 #
4 tháng 5 2019
\(=\frac{5}{3}.\frac{7}{5}.\frac{9}{7}......\frac{91}{89}\)
\(=\frac{91}{3}\)
@@@@@@@@@@@2
9 tháng 11 2017
Ta có: \(A=3+3^2+3^3+...+3^{2008}\)
\(\Rightarrow3A=3^2+3^3+3^4+...+3^{2009}\)
Trừ \(3A-A=3^2+3^3+3^4+...+3^{2009}-3-3^2-3^3-...-3^{2008}\)
\(\Rightarrow2A=3^{2009}-3\)
Mà \(2A=3^x-3\)
\(\Rightarrow3^x=3^{2009}\)
\(\Rightarrow x=2009.\)
Vậy x = 2009.
FT
10 tháng 11 2017
\(a=3+3^2+3^3+...+3^{2008}\)
\(3a=3^2+3^3+3^4+...+3^{2009}\)
\(3a-a=\left(3^2+3^3+3^4+...+3^{2009}\right)-\left(3+3^2+3^3+...+3^{2008}\right)\)
\(2a=3^{2009}-3\)
\(2a+3=3^{2009}=3^x\)
\(x=2009\)
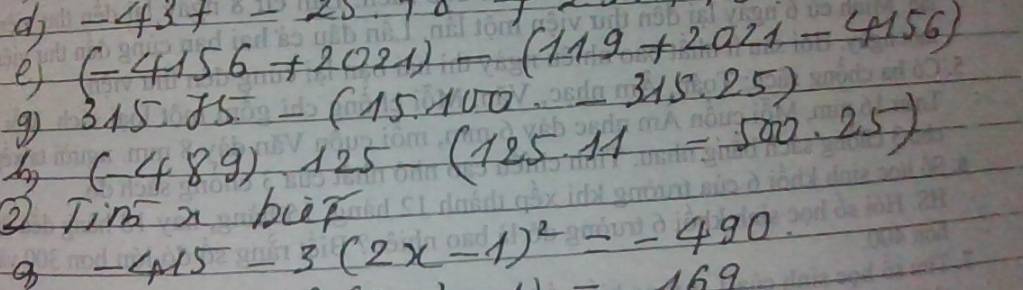
Bài 3:
Vì (d') và (d'') cắt nhau tại một điểm trên trục tung nên ta có:
\(\left\{{}\begin{matrix}m+2< >2\\-m^2+4m-2=m-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< >0\\-m^2+3m=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< >0\\m\left(-m+3\right)=0\end{matrix}\right.\Leftrightarrow m=3\)