Cho tam giác ABC đều, cạnh 2a. Gọi G là trọng tâm của tam giác. Khi đó |AB-GC|=?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H
0
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 12 2021
\(T=\overrightarrow{GA}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)+\overrightarrow{GB}.\overrightarrow{CA}+\overrightarrow{GC}.\overrightarrow{AB}\)
\(=\overrightarrow{AB}\left(\overrightarrow{GC}-\overrightarrow{GA}\right)+\overrightarrow{AC}\left(\overrightarrow{GA}-\overrightarrow{GB}\right)\)
\(=\overrightarrow{AB}\left(\overrightarrow{GC}+\overrightarrow{AG}\right)+\overrightarrow{AC}\left(\overrightarrow{GA}+\overrightarrow{BG}\right)\)
\(=\overrightarrow{AB}.\overrightarrow{AC}+\overrightarrow{AC}.\overrightarrow{BA}\)
\(=0\)
19 tháng 3 2016
Từ giả thiết suy ra với mọi O đều có ?
\(\overrightarrow{OG}=\frac{1}{3}\left(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\right)\) và \(\overrightarrow{OG_1}=\frac{1}{3}\left(\overrightarrow{OA}_1+\overrightarrow{OB_1}+\overrightarrow{OC}_1\right)\)
Mà :
\(\overrightarrow{OG_2=}\frac{1}{3}.\left(\overrightarrow{OGa}+\overrightarrow{OG_b}+\overrightarrow{OG_c}\right)\)
\(=\frac{1}{3}\left(\frac{1}{3}\left(\overrightarrow{OA}+\overrightarrow{OB_1}+\overrightarrow{OC_1}\right)+\frac{1}{3}\left(\overrightarrow{OB}+\overrightarrow{OC_1}+\overrightarrow{OA_1}\right)+\frac{1}{3}\left(\overrightarrow{OC}+\overrightarrow{OA_1}+\overrightarrow{OB_1}\right)\right)\)
\(=\frac{1}{3}\left(\frac{1}{3}\left(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\right)+\frac{2}{3}\left(\overrightarrow{OA_1}+\overrightarrow{OB_1}+\overrightarrow{OC}_1\right)\right)\)
\(=\frac{1}{3}\overrightarrow{OG}+\frac{2}{3}\overrightarrow{OG_1}\)
Suy ra :
\(3\overrightarrow{OG_2}=\overrightarrow{OG}+2\overrightarrow{OG_1}\) với mọi O. Điều này có nghĩa là \(G,G_1,G_2\) thẳng hàng => Điều phải chứng minh
5 tháng 12 2023
Kẻ \(\overrightarrow{AH}=\overrightarrow{GC}\)
ΔABC đều có G là trọng tâm
nên G là tâm đường tròn nội tiếp ΔABC
=>AG,CG,BG lần lượt là phân giác của góc \(\widehat{BAC};\widehat{ACB};\widehat{ABC}\)
ΔABC đều
=>\(\widehat{BAC}=\widehat{ACB}=\widehat{ABC}=60^0\)
AG là phân giác của góc BAC
=>\(\widehat{BAG}=\widehat{CAG}=\dfrac{1}{2}\cdot\widehat{BAC}=\dfrac{1}{2}\cdot60^0=30^0\)
CG là phân giác của góc ACB
=>\(\widehat{ACG}=\widehat{BCG}=\dfrac{1}{2}\cdot\widehat{ACB}=30^0\)
Xét ΔGAC có \(\widehat{AGC}+\widehat{GAC}+\widehat{GCA}=180^0\)
=>\(\widehat{AGC}+30^0+30^0=180^0\)
=>\(\widehat{AGC}=120^0\)
\(\overrightarrow{AH}=\overrightarrow{GC}\)
=>AH//GC và AH=GC
Xét tứ giác AHCG có
AH//CG
AH=CG
Do đó: AHCG là hình bình hành
=>\(\widehat{GAH}+\widehat{AGC}=180^0\)
=>\(\widehat{GAH}=180^0-120^0=60^0\)
ΔABC đều có G là trọng tâm
nên \(AG=CG=BG=\dfrac{a\sqrt{3}}{3}=\dfrac{2\sqrt{3}\cdot\sqrt{3}}{3}=2\)
\(\overrightarrow{AB}-\overrightarrow{GC}=\overrightarrow{AB}-\overrightarrow{AH}=\overrightarrow{AB}+\overrightarrow{HA}=\overrightarrow{HB}\)
\(\widehat{BAH}=\widehat{BAG}+\widehat{GAH}=30^0+60^0=90^0\)
=>ΔABH vuông tại A
AH=CG
mà 2
nên AH=2
ΔABH vuông tại A
=>\(BH^2=AB^2+AH^2\)
=>\(BH^2=\left(2\sqrt{3}\right)^2+2^2=16\)
=>BH=4
=>\(\left|\overrightarrow{AB}-\overrightarrow{GC}\right|=\left|\overrightarrow{HB}\right|=HB=4\)
CM
6 tháng 9 2017
Đáp án B
A’ = V G ; k ( A ) => − 2 G A ' → = G A → =>Tỉ số vị tự k = – 2
CM
21 tháng 1 2018
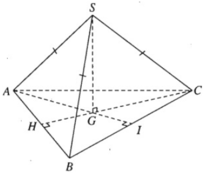
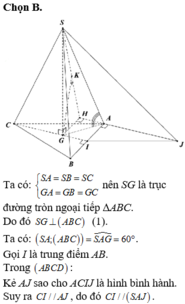
a) SG là trục đường tròn ngoại tiếp tam giác đều ABC nên SG ⊥ (ABC). Ta có
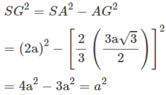
Vậy khoảng cách từ S tới mặt phẳng (ABC) là độ dài của đoạn SG = a
Ta có CG ⊥ AB tại H. Vì GH là đoạn vuông góc chung của AB và SG, do đó
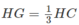
mà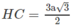 
nên 