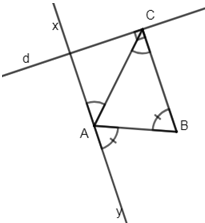
Cho \(\widehat{yBC}=\widehat{ACB}+\widehat{xAC}\) . CMR:...
Đọc tiếp
Cho \(\widehat{yBC}=\widehat{ACB}+\widehat{xAC}\) . CMR: Ax//By
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 8 2017
Gọi By' là tia đối của tia By.
Gọi I là giao điểm của AC và yy'
By//Ax (gt) nên By'//Ax
Do By'//Ax nên xAC=AIy' ( so le trong)
Ta lại có: AIy=BIC ( đối đỉnh)
Do yBC là góc ngoài tại đỉnh B của tam giác BCI nên:
yBC=BIC+ACB
Mà xAC=AIy'
BIC=AIy'
=> xAC=BIC
Do đó yBC=xAC+ACB (đpcm)
NX
9 tháng 8 2023
a) Ta có: mà hai góc đó là hai góc so le trong nên
suy ra (1)
mà hai góc đó là hai góc so le trong nên suy ra (2)
Từ (1) và (2) suy ra Ax và Ay cùng // BC.
Lại có tia Ax thuộc mặt phẳng bờ AB có chứa điểm C, tia Ay thuộc mặt phẳng
bờ AB không chứa điểm C
Ax và Ay là hai tia đối nhau.
b) Vì Ax và Ay là hai tia đối nhau (cmt) mà và
nên suy ra
Mà nên suy ra
23 tháng 5 2022
`a,`
Xét $\Delta OAC$ và $\Delta ABC$ ta có `:`
`OA=OB(gt)`
\(\widehat{AOC}=\widehat{BOC}\) `( Oz` là tia phân giác \(\widehat{B}\) `)`
Chung `Oz`
`=>` $\Delta OAC$ `=` $\Delta ABC$ `(c.g.c)`
`=>` `{(\hat{OAC}=\hat{OBC} \text{( 2 góc tương ứng )} ),(AC=BC \text{ (2 cạnh tương ứng)}):}`
Từ `\hat{OAC}=\hat{OBC}`
`=>` `\hat{xAC}=\hat{yBC}` `(` kề bù với `2` góc bằng nhau `)`
`b,` Xem lại đề bài `: OC=OB?`
1 tháng 11 2022
a: \(\widehat{EAB}=\dfrac{180^0-\widehat{BAC}}{2}=\dfrac{\widehat{ABC}+\widehat{ACB}}{2}\)
\(\widehat{EBA}=180^0-\widehat{ABC}\)
=>\(\widehat{EAB}+\widehat{EBA}=\dfrac{1}{2}\widehat{ABC}+\dfrac{1}{2}\widehat{ACB}+180^0-\widehat{ABC}=-\dfrac{1}{2}\widehat{ABC}+\dfrac{1}{2}\widehat{ACB}+180^0\)
=>\(\widehat{E}=180^0+\dfrac{1}{2}\widehat{ABC}-\dfrac{1}{2}\widehat{ACB}-180^0=\dfrac{1}{2}\widehat{ABC}-\dfrac{1}{2}\widehat{ACB}\)
=>góc E=1/2góc BAx-góc C
b: góc E=1/2góc BAx-góc BAx+góc B
=góc B-1/2góc xAB
c: góc E=1/2góc ABC-1/2góc ACB
=>2*góc E=góc ABC-góc ACB
31 tháng 7 2022
góc xAC=180-100=80 độ
=>góc yAC=80/2=40 độ=góc ACB
=>Ay//BC
30 tháng 10 2018
a. Ta có: \(\widehat{HAB}+\widehat{HAD}=\widehat{BAD}\)
\(\widehat{HAC}-\widehat{HAD}=\widehat{DAC}\)
Vì AD là tia phân giác của góc BAC => \(\widehat{BAD}=\widehat{DAC}\) =.> ĐPCM
b. Xét tam giác HAC có \(\widehat{AHC}+\widehat{HCA}+\widehat{HAC}=180\text{đ}\text{ộ}\)
=>\(\widehat{HAC}=180^o-\widehat{AHC}-\widehat{HCA}\)
Xét tam giác HAB có \(\widehat{HAB}+\widehat{ABH}+\widehat{BHA}=180^o\)
=> \(\widehat{HAB}=180^o-\widehat{ABH}-\widehat{BHA}\)
Ta có: \(\widehat{HAC}-\widehat{HAB}=180^o-\widehat{AHC}-\widehat{HAC}-\left(180^o-\widehat{ABH}-\widehat{BHA}\right)\)
\(=180^o-90^o-\widehat{HCA}-180^o+\widehat{ABH}+90^o\)
\(=180^o-180^o+90^o-90^o+\widehat{ABH}-\widehat{HCA}\)
\(=\widehat{ABH}-\widehat{HCA}=>\text{Đ}PCM\)
c. Ta có: \(\dfrac{1}{2}\left(\widehat{ABC}-\widehat{ACB}\right)=\dfrac{\widehat{ABC}-\widehat{ACB}}{2}=\dfrac{\widehat{HAC}-\widehat{HAB}}{2}\)
\(=\dfrac{2\widehat{DAH}}{2}=\widehat{DAH}=>\text{Đ}pcm\)
16 tháng 11 2022
a: góc ADC-góc ADB
=góc BAD+góc ABD-góc DAC-góc C
=góc ABC-góc ACB
b: ΔAHD vuông tại H
nên góc HAD+góc ADH=90 độ
=>góc DAH=90 độ-góc ADH
=90 độ-180 độ+góc ADC
=góc ADC-90 độ
Ta có thể chứng minh được tổng ba góc trong một tam giác bằng \(180^o\).
Từ B kẻ đường thẳng song song với tia Ax cắt AC tại D.
Suy ra \(\widehat{xAC}=\widehat{BDC}\) (hai góc so le trong). (1)
Ta có \(\widehat{DBC}+\widehat{BDC}+\widehat{DCB}=180^o\).(2)
mà \(\widehat{yBC}=\widehat{ACB}+\widehat{xAC}\) (3).
Từ (1), (2), (3) suy ra:
\(\widehat{yBC}+\widehat{DBC}=180^o\).
hay tia By nằm trên đường thẳng BD. Từ đó suy ra Ax // By.
thanks bn nhìu nha 😊😊😊