Question

[Phạm Mỹ Dung]

Câu 1.

a) Cho a ≥ 0, b ≥ 0. Chứng minh bất đẳng thức Cauchy:

b) Cho a, b, c > 0. Chứng minh rằng:

c) Cho a, b > 0 và 3a + 5b = 12. Tìm giá trị lớn nhất của tích P = ab.

Câu 2. Cho a + b = 1. Tìm giá trị nhỏ nhất của biểu thức: M = a³ + b³.

Câu 3. Cho a³ + b³ = 2. Tìm giá trị lớn nhất của biểu thức: N = a + b.

Câu 4. Cho a, b, c là các số dương. Chứng minh: a³ + b³ + abc ≥ ab(a + b + c)

Câu 5. Tìm liên hệ giữa các số a và b biết rằng: |a + b| > |a - b|

Câu 6.

a) Chứng minh bất đẳng thức (a + 1)² ≥ 4a

b) Cho a, b, c > 0 và abc = 1. Chứng minh: (a + 1)(b + 1)(c + 1) ≥ 8

Answer 1

[Nguyễn Lê Phước Thịnh]

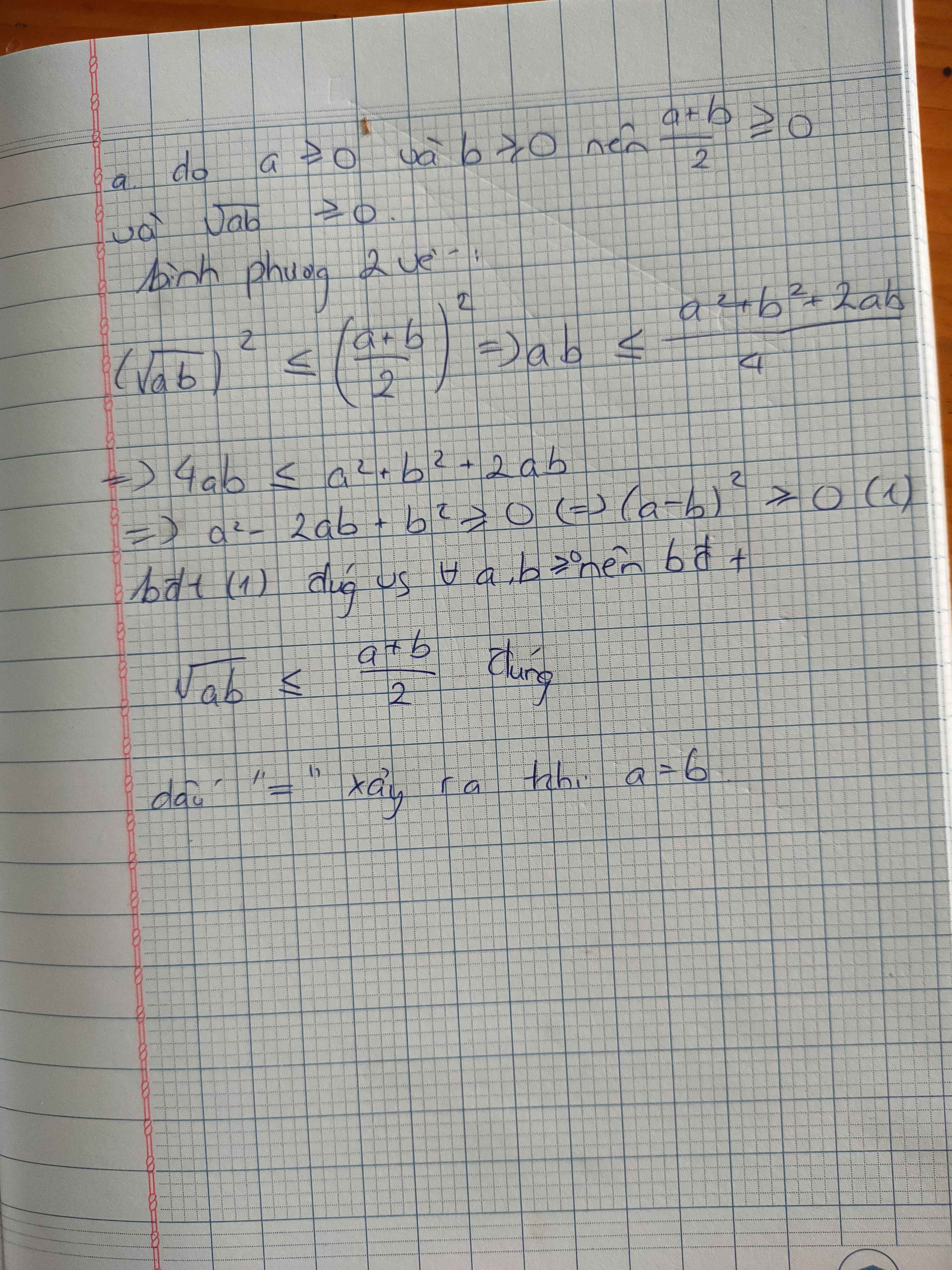
Câu 6: 

a: \(\left(a+1\right)^2>=4a\)

\(\Leftrightarrow a^2+2a+1-4a>=0\)

\(\Leftrightarrow a^2-2a+1>=0\)

\(\Leftrightarrow\left(a-1\right)^2>=0\)(luôn đúng)

b: \(\left\{{}\begin{matrix}a+1\ge2\sqrt{a}\\b+1\ge2\sqrt{b}\\c+1\ge2\sqrt{c}\end{matrix}\right.\)(Theo BĐT COSI)

\(\Leftrightarrow\left(a+1\right)\left(b+2\right)\left(c+1\right)\ge8\sqrt{abc}=8\)