giải phương trình lượng giác :
tan22x.tan23x.tan5x = tan22x - tan23x + tan5x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Cách giải các phương trình lượng giác cơ bản:
+ Phương trình sin x = a.
Nếu |a| > 1 ⇒ phương trình vô nghiệm.
Nếu |a| ≤ 1 ⇒ tìm một cung α sao cho sin α = a.
Khi đó phương trình trở thành sin x = sin α
⇒ Phương trình có nghiệm: 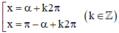
+ Phương trình cos x = a.
Nếu |a| > 1 ⇒ phương trình vô nghiệm.
Nếu |a| ≤ 1 ⇒ tìm một cung α sao cho cos α = a.
Khi đó phương trình trở thành cos x = cos α.
⇒ Phương trình có nghiệm: x = ±α + k2π (k ∈ Z).
+ Phương trình tan x = a.
Tìm một cung α sao cho tan α = a.
Khi đó phương trình trở thành tan x = tan α.
⇒ Phương trình có nghiệm x = α + kπ (k ∈ Z).
+ Phương trình cot x = a
Tìm một cung α sao cho cot α = a.
Khi đó phương trình trở thành cot x = cot α.
⇒ Phương trình có nghiệm x = α + kπ (k ∈ Z).
b) Cách giải phương trình a.sin x + b.cos x = c.
+ Nếu a = 0 hoặc b = 0 ⇒ Phương trình lượng giác cơ bản .
+ a ≠ 0 và b ≠ 0. Chia cả hai vế của phương trình cho  ta được:
ta được:

Ta giải phương trình trên như phương trình lượng giác cơ bản.

`sin(8x+60^o)+sin2x=0`
`<=> sin(8x+60^o) = -sin2x`
`<=> sin(8x+60^o) = sin(-2x)`
\(\Leftrightarrow\left[{}\begin{matrix}8x+60^o=-2x+k.360^o\\8x+60^o=180^o+2x+k.360^o\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-6^o+36^o.k\\x=20^o+60^o.k\end{matrix}\right.\)
Vậy....

=>cosx=pi/2+k2pi
Phương trình này sẽ có nghiệm khi -1<=pi/2+k2pi<=1 và k thuộc Z
=>\(x\in\varnothing\)


\(sin^23x.cos2x+sin^2x=0\)
\(\left(3sinx-4sin^3x\right)^2.cos2x+sin^2x=0\)
\(sin^2x\left[\left(3-4sin^2x\right)^2.cos2x+1\right]=0\)
\(sin^2x\left[\left(1+2cos2x\right)^2.cos2x+1\right]=0\)
\(sin^2x\left(4cos^22x+1\right)\left(cos2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\cos2x=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\text{π}\\2x=k2\text{π}\end{matrix}\right.\)\(\Leftrightarrow x=k\text{π}\)
Ha Hoang , bn ơi từ dòng 4 chuyển sang dòng 5 làm kiểu gì vậy ạ???