Hệ số hạng tử bậc hai của tích (\(\left(\dfrac{1}{5}x-3\right)\left(3x^2-5x+2\right)\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(M\left(x\right)=-2x^5+5x^2+7x^4-5x+8+2x^5-7x^4-4x^2+6\)
\(=\left(-2x^5+2x^5\right)+\left(7x^4-7x^4\right)+\left(5x^2-4x^2\right)-9x+\left(8+6\right)\)
\(=x^2-9x+14\)
\(N\left(x\right)=7x^7+x^6-5x^3+2x^2-7x^7+5x^3+3\)
\(=\left(7x^7-7x^7\right)+x^6-\left(5x^3-5x^3\right)+2x^2+3\)
\(=x^6+2x^2+3\)
b) Đa thức M(x) có hệ số cao nhất là 1
hệ số tự do là 14
bậc 2
Đa thức N(x) có hệ số cao nhất là 1
hệ số tự do là 3
bậc 6

a: \(P\left(x\right)=-5x^4+2x^2-8x+\dfrac{1}{2}\)
\(Q\left(x\right)=4x^4+2x^3-5x^2-6x+\dfrac{3}{2}\)
b: \(A\left(x\right)=-5x^4+2x^2-8x+\dfrac{1}{2}+4x^4+2x^3-5x^2-6x+\dfrac{3}{2}=-x^4+2x^3-3x^2-14x+2\)
\(B\left(x\right)=-5x^4+2x^2-8x+\dfrac{1}{2}-4x^4-2x^3+5x^2+6x-\dfrac{3}{2}=-9x^4-2x^3+7x^2-2x-1\)

a) \(\left( {\dfrac{1}{2}{x^3}} \right).\left( -{4{x^2}} \right) = \left( {\dfrac{1}{2}.(-4)} \right).\left( {{x^3}.{x^2}} \right) = (-2).{x^5}\).
Hệ số: -2
Bậc: 5
b) \(\dfrac{1}{2}{x^3} - \dfrac{5}{2}{x^3} = \left( {\dfrac{1}{2} - \dfrac{5}{2}} \right){x^3} = \dfrac{{ - 4}}{2}.{x^3} = - 2{x^3}\)
Hệ số: -2
Bậc: 3
\(a,\left(\dfrac{1}{2}x^3\right).\left(-4x^2\right)=\left(-4.\dfrac{1}{2}\right).\left(x^3.x^2\right)=-2x^5\\ Hệ.số:-2;bậc:5\\ b,\dfrac{1}{2}x^3-\dfrac{5}{2}x^3=-2x^3\\ Hệ.số:-2;bậc:3\)

\(\left(x-3x\right)^3=\left(-2x\right)^3=-8x^3\)
Hệ số của hạng tử bậc là 3 là -8
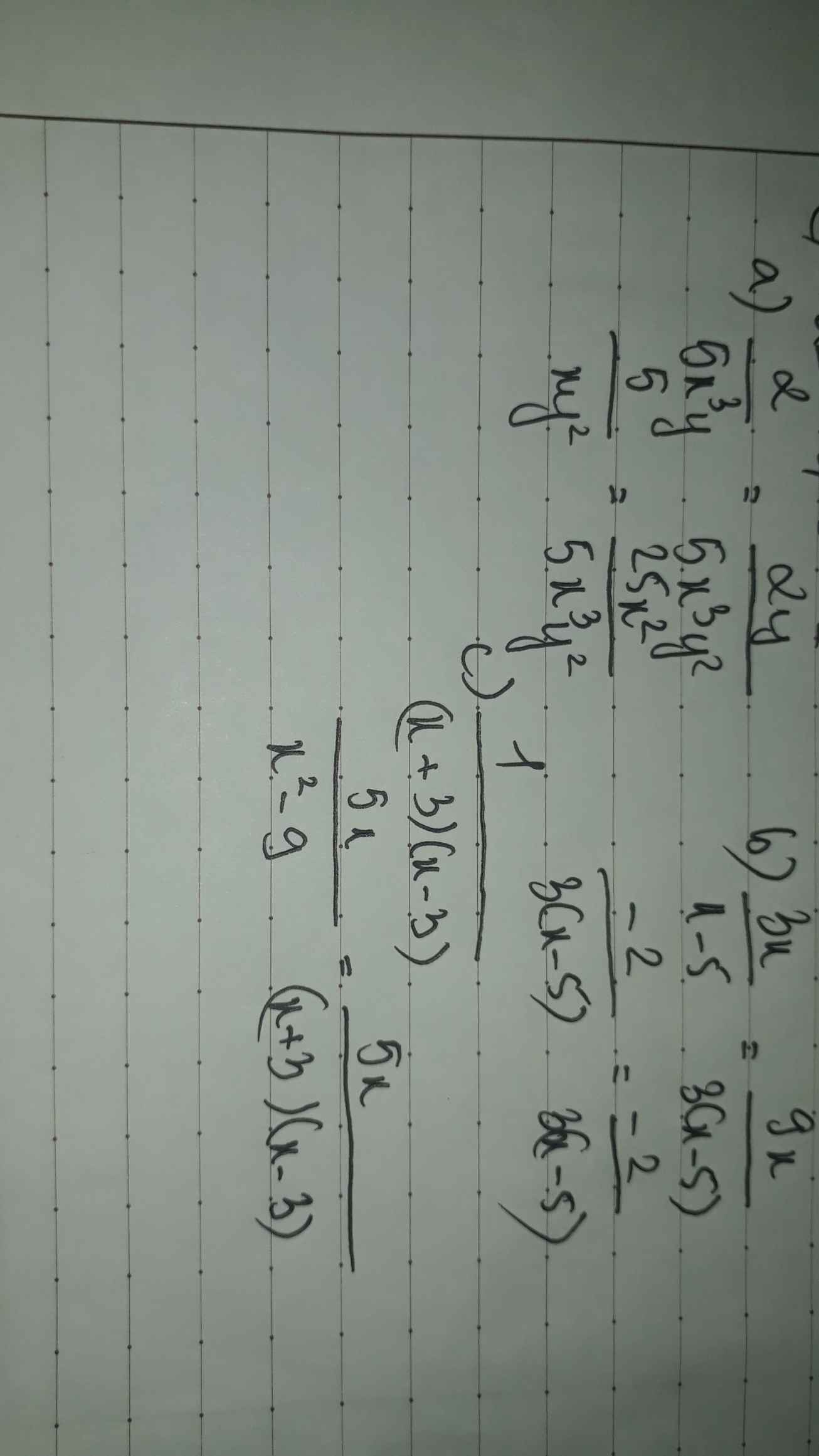

Dễ mà nhân ra ik r` bt