Tứ giác abcd có ca,bd vuông góc với ab,m là trung điểm của ab,dm vuông góc với cm, mh vuông góc với cd.chứng minh cd=ac+bd,tam giác ahb vuông tại h
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 7 2023
a: Xét ΔDBC có BH/BD=BF/BC
=>HF//DC
=>EI vuông góc HF(1)
Xét ΔBAC có BE/BA=BF/BC
nên EF//AC
=>EF vuông góc HI(2)
Từ (1), (2) suy ra I là trực tâm của ΔHEF
b: I là trực tâm của ΔHEF
=>FI vuông góc EH
Xét ΔBAD có BE/BA=BH/BD
nên EH//AD
=>FI vuông góc AD
KN
11 tháng 10 2020
Ta có M, N lần lượt là trung điểm của AB, AD nên MN là đường trung bình của ∆ABD => MN // BD
Mà AC⊥BD nên MN⊥AC hay LA⊥MN (1)
N, L lần lượt là trung điểm của AD, AC nên NL là đường trung bình của ∆ADC => NL // DC
Mà MH⊥DC nên NL⊥MH (2)
Từ (1) và (2) suy ra H là trực tâm của tam giác MNL (đpcm)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 1 2022
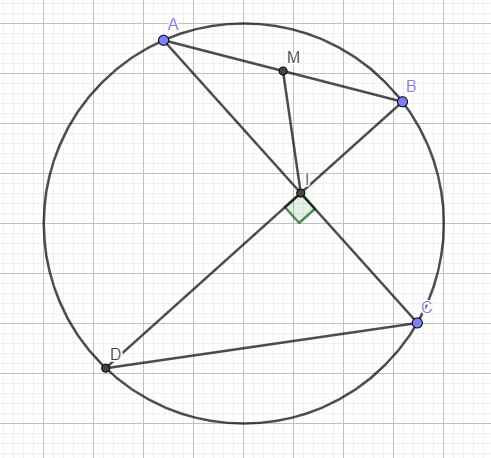
M là trung điểm AB \(\Rightarrow\overrightarrow{IM}=\dfrac{1}{2}\left(\overrightarrow{IA}+\overrightarrow{IB}\right)\)
\(\Rightarrow2\overrightarrow{IM}.\overrightarrow{DC}=\left(\overrightarrow{IA}+\overrightarrow{IB}\right).\left(\overrightarrow{DI}+\overrightarrow{IC}\right)=\overrightarrow{IA}.\overrightarrow{DI}+\overrightarrow{IB}.\overrightarrow{IC}+\overrightarrow{IA}.\overrightarrow{IC}+\overrightarrow{IB}.\overrightarrow{DI}\)
\(=\overrightarrow{IA}.\overrightarrow{IC}+\overrightarrow{IB}.\overrightarrow{DI}=-IA.IC+IB.DI\)
Mặt khác do 2 tam giác vuông DIC và AIB đồng dạng (\(\widehat{IAB}=\widehat{IDC}\) cùng chắn BC)
\(\Rightarrow\dfrac{IA}{ID}=\dfrac{IB}{IC}\Rightarrow IA.IC=IB.ID\Rightarrow-IA.IC+IB.ID=0\)
\(\Rightarrow2\overrightarrow{IM}.\overrightarrow{DC}=0\Rightarrow IM\perp DC\)
