Tìm n € z để :
2n2+5n-1 chia hết cho 2n-1
Mình cần gấp giúp mk vs nha
Thanks nhìu !
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1./ Do 2n + 1 là số lẻ nên n2 - 2n + 4 chia hết cho 2n+1 thì 4(n2 - 2n + 4) cũng chia hết cho 2n + 1 (nhân số 4 chẵn ko tăng thêm ước cho 2n + 1)
mà: B = 4(n2 - 2n + 4) = 4n2 + 4n + 1 - 12n - 6 + 21 = (2n + 1)2 - 6(2n+1) + 21 = (2n + 1)(2n + 1 - 6) +21 = (2n + 1)(2n - 5) + 21
=> B chia hết cho 2n + 1 <=> 21 chia hết cho 2n + 1.
=> 2n + 1 thuộc U (21) = {-21;-7;-3;-1;1;3;7;21}
Khi đó n = -11; -4 ; -2; -1 ; 0 ; 1; 3 ; 10.
2./ C = 2n2 + 8n + 11 = 2n2 +4n + 4n + 8 + 3 = 2n(n + 2) + 4(n + 2) + 3 = (n + 2)(2n + 4) + 3
để 2n2 + 8n + 11 chia hết cho n + 2 thì n + 2 phải là U(3) = {-3; -1; 1; 3)
Khi đó n = -5 ; -3 ; -1 ; 1

Cách 1: Thực hiện phép chia 2n2 – n + 2 cho 2n + 1 ta có:
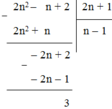
2n2 – n + 2 chia hết cho 2n + 1
⇔ 3 ⋮ (2n + 1) hay (2n + 1) ∈ Ư(3)
⇔ 2n + 1 ∈ {±1; ±3}
+ 2n + 1 = 1 ⇔ 2n = 0 ⇔ n = 0
+ 2n + 1 = -1 ⇔ 2n = -2 ⇔ n = -1
+ 2n + 1 = 3 ⇔ 2n = 2 ⇔ n = 1
+ 2n + 1 = -3 ⇔ 2n = -4 ⇔ n = -2.
Vậy n ∈ {-2; -1; 0; 1.}
Cách 2:
Ta có:
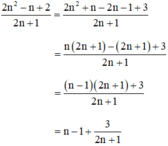
2n2 – n + 2 chia hết cho 2n + 1
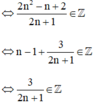
⇔ 2n + 1 ∈ Ư(3) = {±1; ± 3}.
+ 2n + 1 = 1 ⇔ 2n = 0 ⇔ n = 0
+ 2n + 1 = -1 ⇔ 2n = -2 ⇔ n = -1
+ 2n + 1 = 3 ⇔ 2n = 2 ⇔ n = 1
+ 2n + 1 = -3 ⇔ 2n = -4 ⇔ n = -2.
Vậy n ∈ {-2; -1; 0; 1.}
Chú ý: Đa thức A chia hết cho đa thức B khi phần dư của phép chia bằng 0.

Thực hiện phép chia 2n2 – n + 2 cho 2n + 1 ta có:
2n^2 - n + 2 2n + 1 n - 1 _ 2n^2 + n -2n + 2 _ -2n - 1 3
2n2 – n + 2 chia hết cho 2n + 1
<=> 3 \(⋮\)( 2n + 1 ) hay ( 2n + 1 ) \(\in\) Ư(3)
<=> 2n + 1 \(\in\) {\(\pm\)1; \(\pm\)3 }
+ 2n + 1 = 1 <=> 2n = 0 <=> n = 0
+ 2n + 1 = -1 <=> 2n = -2 <=> n = -1
+ 2n + 1 = 3 <=> 2n = 2 <=> n = 1
+ 2n + 1 = -3 <=> 2n = -4 <=> n = -2.
Vậy n \(\in\) { -2 ; -1 ; 0 ; 1 }

ta có : \(6n-3=3\times\left(2n-2\right)+3\) chia hết cho 2n-2 khi
3 chia hết cho 2n-2
mà 2n-2 là số chẵn nên 3 không thể chia hết cho 2n-2 vậy không tồn tại số tự nhiên thỏa mãn

a) Sử dụng định lí Fermat nhỏ: Với mọi \(n\inℕ\), \(p\ge2\)là số nguyên tố. Ta luôn có \(n^p-n⋮7\)
Dễ thấy 7 là số nguyên tố. Do đó \(n^7-n⋮7\)
Có thể sự dụng pp quy nạp toán học hay biến đổi đẳng thức rồi sử dụng pp xét từng giá trị tại 7k+n với 7>n>0
b)Ta có: \(2n^3+3n^2+n=2n^3+2n^2+n^2+n\)
\(=n^2\left(2n+1\right)+n\left(2n+1\right)\)
\(=n\left(n+1\right)\left(2n+1\right)\)
Ta thấy n(n+1) chia hết 2. Chỉ cần chứng minh thêm đằng thức trên chia hết cho 3
Đặt n=3k+1 và n=3k+2. Tự thế vài và CM
c) Tương tự: \(n^5-5n^3+4n=n^3\left(n^2-1\right)-4n\left(n^2-1\right)\)
\(=\left(n-1\right)\left(n+1\right)\left(n^3-4n\right)\)
\(=\left(n-1\right)\left(n+1\right)n\left(n^2-4\right)\)
\(=n\left(n-1\right)\left(n+1\right)\left(n-2\right)\left(n+2\right)\)
Sắp xếp lại cho trật tự: \(\left(n-2\right)\left(n-1\right)n\left(n+1\right)\left(n+2\right)\)
Dễ thấy đẳng thức trên chia hết cho 5
Mà ta có: \(n\left(n+1\right)\left(n+2\right)⋮3\)
Và \(\left(n-1\right)n\left(n+1\right)\left(n+2\right)⋮4\)
Và tích của hai số bất kì cũng chia hết cho 2
Vậy đẳng thức trên chia hết cho 3.4.2.5=120
Cậu cuối bn chứng minh cách tương tự. :)
\(2n^2+5n-1=2n^2-n+6n-3+2=n\left(2n-1\right)+3\left(2n-1\right)+2\)suy ra \(2n-1\inƯ\left(2\right)\)
+) \(2n-1=1\Rightarrow n=1\)
+) \(2n-1=-1\Rightarrow n=0\)
+) \(2n-1=2\Rightarrow n=\dfrac{3}{2}\) (loại)
+)\(2n-1=-2\Rightarrow n=\dfrac{-1}{2}\) (loại)
Vậu các giá trị của n thỏa mãn đề bài là \(n=0;n=1\)