Hai điện tích +q và-q (q>0) đặt tại 1 điểm A và B với AB=2cm. M là một điểm nằm trên đường trung trực của AB cách AB một đoạn x
a. Xác định vectơ cường độ điện trường tại M
b. Xác định x để cường độ điện trường tại M cực đại, tính giá trị đó
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
21 tháng 12 2018
Đáp án: C
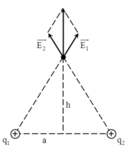
Cường độ điện trường tại điểm M là
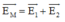
Trong đó E 1 → , E 2 → là cường độ điện trường do q 1 và q 2 gây ra tại M:
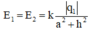
Suy ra: Cường độ điện trường tổng hợp tại M:
E M = 2 E 1 cos α = 2 k q h a 2 + h 2 1,5 V / m
Áp dụng bất đẳng thức Cô-si, ta có:
a 2 + h 2 = a 2 2 + a 2 2 + h 2 ≥ 3 a 4 h 2 4 3 ⇒ a 2 + h 2 3 ≥ 27 4 a 4 h 2
⇒ a 2 + h 2 3 2 ≥ 3 3 2 a 2 h
Vậy E M ≤ 2 k q h 3 3 2 a 2 h = 4 k q 3 3 a 2
EM cực đại khi h = a 2 ⇒ E M max = 4 k q 3 3 a 2
VT
19 tháng 7 2018
a) Các điện tích q 1 v à q 2 gây ra tại M các véc tơ cường độ điện trường E 1 → và E 2 → có phương chiều như hình vẽ.
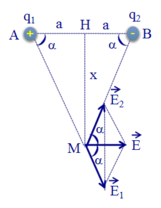
Có độ lớn: E 1 = E 2 = k q ε ( a 2 + x 2 )
Cường độ điện trường tổng hợp tại M do các điện tích q 1 v à q 2 gây ra là:
E → = E 1 → + E 2 → ; có phương chiều như hình vẽ.
Có độ lớn: 2 E 1 cos α = 2 . k q ( a 2 + x 2 ) a a 2 + x 2 = 2 k q a ( a 2 + x 2 ) 3 2
b) Theo câu a ta có: E = 2 k q a ( a 2 + x 2 ) 3 2 ; để E có giá trị cực đại thì mẫu số phải có giá trị cực tiểu mà mẫu số có giá trị cực tiểu khi x = 0 tức là M trùng với H.
9 tháng 8 2021
a) Vector cường độ điện trường tại M có phương và chiều được xác định như hình vẽ
Ta có \(|\overrightarrow{E_A}|=|\overrightarrow{MC}|=\frac{kq}{MA^2}=\frac{kq}{a^2+h^2}\)
\(\frac{MC}{MA}=\frac{MN}{2MP}\Rightarrow MN=\left|\overrightarrow{E_{AB}}\right|=\frac{2MC.MP}{MA}=\frac{2kqh}{\left(a^2+h^2\right)\sqrt{a^2+h^2}}\left(\frac{V}{m}\right)\)
b) Áp dụng BĐT Cauchy ta có:
\(E_{AB}=\frac{2kqh}{\sqrt{\left(a^2+h^2\right)^3}}=\frac{2kqh}{\sqrt{\left(\frac{a^2}{2}+\frac{a^2}{2}+h^2\right)^3}}\)
\(\le\frac{2kqh}{\sqrt{\left(3\sqrt[3]{\frac{a^4h^2}{4}}\right)^3}}=\frac{4kq}{3\sqrt{3}a^2}\)(không đổi)
Đạt được khi \(h=\frac{a\sqrt{2}}{2}.\)
VT
3 tháng 9 2019
a) Các điện tích q1 và q2 gây ra tại M các véc tơ cường độ điện trường E 1 → và E 2 → có phương chiều như hình vẽ:
Có độ lớn: E 1 = E 2 = k q ( a 2 + x 2 ) .
Cường độ điện trường tổng hợp tại M do các điện tích q 1 v à q 2 gây ra là:
E → = E 1 → + E 2 → ; có phương chiều như hình vẽ.
Có độ lớn: E = E 1 cos α + E 2 cos α = 2 E 1 cos α = 2 . k q ( a 2 + x 2 ) . x a 2 + x 2 = 2 k q x ( a 2 + x 2 ) 3 2
b) Theo câu a ta có E = 2 k q x ( a 2 + x 2 ) 3 2 = 2 k q a 2 x 2 3 + x 4 3 3 2 .
Để E có giá trị cực đại thì mẫu số phải có giá trị cực tiểu mà mẫu số có giá trị cực tiểu khi a 2 x 2 3 = x 4 3 (theo bất đẳng thức Côsi) ð a 2 = x 2 hay x = a.
ta có |qA|=|qB|,AC=BC
===> Eac=Ebc=KqA÷AC^2
vẽ hình đc vecto tổng hợp tại C song song với AB và cùng hướng với vecto AB
vì tam giác ABC cân tại C có
Ec=Eac√(2+2cos(180-ACB))
để Ec MAX thì Eac MAX
hay Eac = KqA÷AC^2
===>AC^2 MIN
ta có AC^2=AI^2+IC^2
áp dung bdt với ta có
AI^2+IC^2>=2√AI^2×IC^2
dấu bàng xảy ra khi AI=IC
vậy để Ec MAX thì IC=AI=1