cho hình bình hành ABCD.Gọi I và K lần lượt là trung điểm của CD,AB. chứng minh tứ giác AKID là hình bình hành
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 1 2023
a: ABCD là hình bình hành ròi nha bạn
b: Xét tứ giác AKCH co
AK//HC
AK=HC
Do đó: AKCH là hình bình hành
=>AH//KC
Xét ΔDQC có
H là trung điểm của DC
HP//QC
Do đó: P là trung điểm của DQ
Xét ΔABP có
K là trung điểm của BA
KQ//AP
Do đó: Q là trung điểm củaBP
=>DP=PQ=QB
15 tháng 12 2023
a: Ta có: ABCD là hình bình hành
=>AB=CD(1)
Ta có: E là trung điểm của AB
=>\(EA=EB=\dfrac{AB}{2}\left(2\right)\)
Ta có: F là trung điểm của CD
=>\(FC=FD=\dfrac{CD}{2}\left(3\right)\)
Từ (1),(2),(3) suy ra EA=EB=FC=FD
Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
b: Xét tứ giác AEFD có
AE//FD
AE=FD
Do đó: AEFDlà hình bình hành
Hình bình hành AEFD có \(AE=AD\left(=\dfrac{AB}{2}\right)\)
nên AEFD là hình thoi
c: Xét tứ giác EBCF có
BE//FC
BE=FC
Do đó: EBCF là hình bình hành
Hình bình hành EBCF có \(EB=BC\left(=\dfrac{AB}{2}\right)\)
nên EBCF là hình thoi
=>EC\(\perp\)BF tại trung điểm của mỗi đường
=>EC\(\perp\)BF tại K và K là trung điểm chung của EC và BF
Ta có: AEFD là hình thoi
=>AF\(\perp\)ED tại trung điểm của mỗi đường
=>AF\(\perp\)ED tại I và I là trung điểm chung của AF và ED
Ta có: AEFD là hình thoi
=>EF=AD
mà AD=DC/2
nên EF=DC/2
Xét ΔEDC có
EF là đường trung tuyến
\(EF=\dfrac{CD}{2}\)
Do đó: ΔEDC vuông tại E
Xét tứ giác EIFK có
\(\widehat{EIF}=\widehat{EKF}=\widehat{IEK}=90^0\)
=>EIFK là hình chữ nhật
d: Để EIFK là hình vuông thì FI=FK
mà \(FI=\dfrac{FA}{2};FK=\dfrac{FB}{2}\)
nên FA=FB
=>ΔFAB cân tại F
Ta có: ΔFAB cân tại F
mà FE là đường trung tuyến
nên FE\(\perp\)AB
ta có: FE\(\perp\)AB
FE//AD
Do đó: AD\(\perp\)AB
8 tháng 11 2021
a: Xét tứ giác BMDN có
BM//DN
BM=DN
Do đó: BMDN là hình bình hành
13 tháng 7 2023
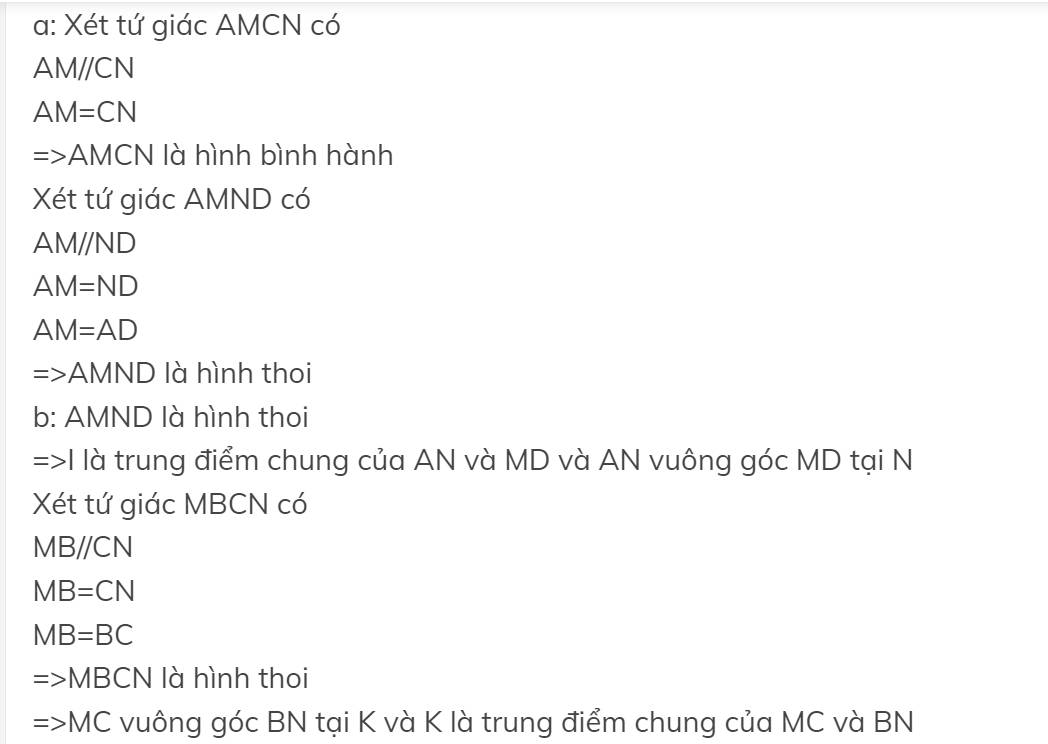
a: Xét tứ giác AMCN có
AM//CN
AM=CN
=>AMCN là hình bình hành
Xét tứ giác AMND có
AM//ND
AM=ND
AM=AD
=>AMND là hình thoi
b: AMND là hình thoi
=>I là trung điểm chung của AN và MD và AN vuông góc MD tại N
Xét tứ giác MBCN có
MB//CN
MB=CN
MB=BC
=>MBCN là hình thoi
=>MC vuông góc BN tại K và K là trung điểm chung của MC và BN
Xét ΔMDC có
MN là trung tuyến
MN=DC/2
=>ΔMDC vuông tại M
Xét tứ giác MINK có
góc MIN=góc MKN=góc IMK=90 độ
=>MINK là hình chữ nhật
c: Xét ΔMDC có MI/MD=MK/MC
nên IK//DC
25 tháng 12 2021
Bài 8:
a: Xét tứ giác AEFD có
AE//FD
AE=FD
Do đó: AEFD là hình bình hành
mà AE=AD
nên AEFD là hình thoi
24 tháng 10 2021
a: Xét tứ giác AECK có
AK//CE
AK=CE
Do đó: AECK là hình bình hành
23 tháng 11 2021
a) Ta có: \(AB=DC,AB//CD\)(ABCD là hình bình hành)
Mà \(K,E\in AB,CD;AK=\dfrac{1}{2}AB;CE=\dfrac{1}{2}CD\)
\(\Rightarrow AK=CE\) và \(AK//CE\)
=> AECK là hình bình hành
b) Ta có: O là giao điểm 2 đường chéo AC và BD
=> O là trung điểm AC
=> O là trung điểm KE(AECK là hình bình hành)
=> E,O,K thẳng hàng