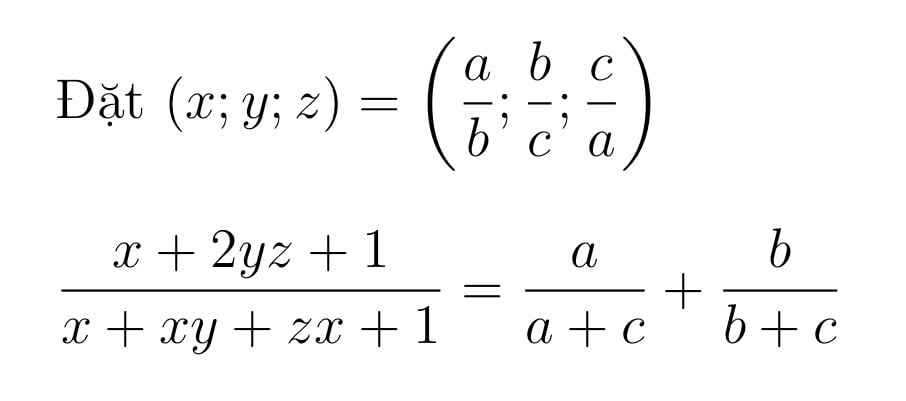biết các số nguyên dương x, y, z thỏa mãn hệ phương trình :x²+xy+(y²/3)=25, (y²/3)+z²=9, z²+xz+x²=16. tính A=xy+2yz+3zx
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
K
11 tháng 9 2021
Ta có \(\frac{x+2xy+1}{x+xy+xz+1}=\frac{x+2xy+xyz}{x+xy+xz+xyz}=\frac{1+2y+yz}{\left(y+1\right)\left(z+1\right)}\)
Tương tự => \(M=\frac{1+2y+yz}{\left(y+1\right)\left(z+1\right)}+\frac{1+2z+zx}{\left(1+x\right)\left(z+1\right)}+\frac{1+2x+xy}{\left(1+x\right)\left(y+1\right)}\)
=> \(M=\frac{\left(1+2y+yz\right)\left(1+x\right)+\left(1+2z+zx\right)\left(1+y\right)+\left(1+2x+xy\right)\left(1+z\right)}{\left(1+x\right)\left(1+y\right)\left(1+z\right)}\)
=>\(M=\frac{6+3\left(x+y+z\right)+3\left(xy+yz+xz\right)}{2+\left(x+y+z\right)+\left(xy+yz+xz\right)}=3\)
LK
1
27 tháng 4 2020
từ giả thiết ta có : z = 6 - x - y
Ta có : \(A=xy+z\left(2y+3x\right)=xy+\left(6-x-y\right)\left(2y+3x\right)\)
\(=-3x^2-2y^2-4xy+18x+12y\)
Do đó : \(3A=-9x^2-6y^2-12xy+54x+36y=-9x^2-6x\left(2y-9\right)-6y^2+36y\)
\(=-\left(3x+2y-9\right)^2-2y^2+81\le81\)
\(\Rightarrow A\le27\)
Vậy giá trị lớn nhất của A là 27 \(\Leftrightarrow\hept{\begin{cases}3x+2y-9=0\\y=0\end{cases}\Leftrightarrow x=3;y=0;z=3}\)
CG
0
NI
1
14 tháng 2 2022
\(xy+2yz+3zx=xy+zx+2yz+2zx=x\left(y+z\right)+2z\left(y+x\right)=x.\left(-x\right)+2z.\left(-z\right)=-x^2-2z^2\le0\)-Dấu bằng xảy ra \(\Leftrightarrow x=y=z=0\)