Giup mik giai nay ik mn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: AK<AQ
=>K nằm giữa A và Q
=>AK+KQ=AQ
=>KQ=1cm
b: AK và AC là hai tia đối nhau
=>A nằm giữa K và C
mà AK=AC
nen A là trung điểm của KC
c: BK=1,5+3=4,5cm>AQ


Bài làm của mk nek:
2x+3x=5
=> x.(2+3)=5
=> x.5=5
=> x=5:5
=> x=1


1 plays
2 are reading
3 sing
4 do - do, help
5 is teaching
7 visited
8 doesn't like
9 watch
10 gets - has - brushes - goes - has
11 played - was
12 met
13 are going to have
14 did - do , planted
15 didn't come
16 paint
17 taught
18 have never been
19 takes
20 have - had
21 received
22 is going to invite
23 is waiting
24 talked
25 is going to travel
26 went - didn't buy
27 doesn't learn - will fail
28 washes
29 will be - watches
30 will phone
2 are reading
3 sings
4 do - do - help
5 is teaching
7 visited
8 doesn't like
9 watch
10 gets - has
6. 10 brushes - goes
6. 30 has
11 played - was
12 met
13 will have
14 did - do - planted
15 didn't come
16 paint
17 taught

uses crt;
var a:array[1..100]of integer;
n,i,kt,j:integer;
begin
clrscr;
write('Nhap n='); readln(n);
for i:=1 to n do
begin
write('A[',i,']='); readln(a[i]);
end;
writeln('Cac so nguyen duong la: ');
for i:=1 to n do
if a[i]>0 then write(a[i]:4);
writeln;
writeln('Cac so nguyen to la: ');
for i:=1 to n do
if a[i]>1 then
begin
kt:=0;
for j:=2 to a[i]-1 do
if a[i] mod j=0 then kt:=1;
if kt=0 then write(a[i]:4);
end;
readln;
end.


Bài 1. (a) Điều kiện: \(x\ne\pm1\).
Ta có: \(A=\left(\dfrac{x-2}{x-1}-\dfrac{x+3}{x+1}+\dfrac{3}{x-1}\right):\left(1-\dfrac{x+3}{x+1}\right)\)
\(=\left(\dfrac{x-2+3}{x-1}-\dfrac{x+3}{x+1}\right):\dfrac{x+1-\left(x+3\right)}{x+1}\)
\(=\left(\dfrac{x+1}{x-1}-\dfrac{x+3}{x+1}\right):\dfrac{x+1-x-3}{x+1}\)
\(=\dfrac{\left(x+1\right)^2-\left(x+3\right)\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}:\dfrac{-2}{x+1}\)
\(=\dfrac{x^2+2x+1-x^2-2x+3}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{-2}\)
\(=\dfrac{4}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{-2}=\dfrac{2}{1-x}\)
Vậy: \(A=\dfrac{2}{1-x}\)
(b) \(A=3\Leftrightarrow\dfrac{2}{1-x}=3\)
\(\Rightarrow1-x=\dfrac{2}{3}\Leftrightarrow x=\dfrac{1}{3}\left(TM\right)\)
Vậy: \(x=\dfrac{1}{3}\)
Bài 2. (a) Phương trình tương đương với:
\(\dfrac{3\left(3x-2\right)}{12}+\dfrac{6\left(x+3\right)}{12}=\dfrac{4\left(x-1\right)}{12}+\dfrac{x+1}{12}\)
\(\Rightarrow3\left(3x-2\right)+6\left(x+3\right)=4\left(x-1\right)+x+1\)
\(\Leftrightarrow9x-6+6x+18=4x-4+x+1\)
\(\Leftrightarrow10x=-15\Leftrightarrow x=-\dfrac{3}{2}\)
Vậy: Phương trình có tập nghiệm \(S=\left\{-\dfrac{3}{2}\right\}\).
(b) Điều kiện: \(x\ne\pm1\). Phương trình tương đương với:
\(\dfrac{2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}+\dfrac{2\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}=\dfrac{2x^2+2}{\left(x+1\right)\left(x-1\right)}\)
\(\Rightarrow2\left(x+1\right)+2\left(x-1\right)=2x^2+2\)
\(\Leftrightarrow2x+2+2x-2=2x^2+2\)
\(\Leftrightarrow2x^2-4x+2=0\Leftrightarrow2\left(x^2-2x+1\right)=0\)
\(\Leftrightarrow2\left(x-1\right)^2=0\Rightarrow x-1=0\Leftrightarrow x=1\left(KTM\right)\)
Vậy: Phương trình có tập nghiệm \(S=\varnothing\)

\(x+\frac{1}{4}=\frac{1}{64}\)
\(x=\frac{1}{64}-\frac{1}{4}\)
\(x=-\frac{15}{64}\)
Vậy x = -15/64
hok tốt
==.==

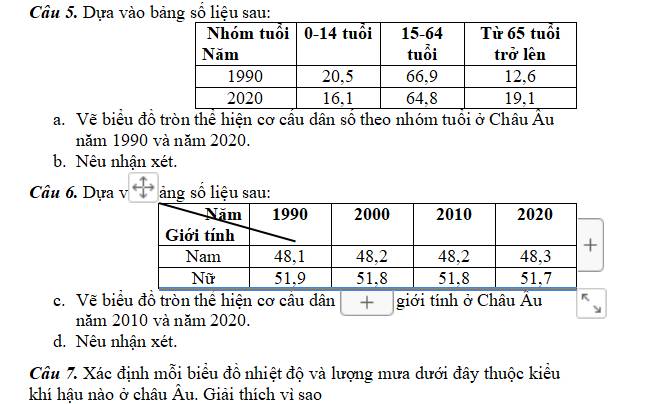

 mn giup mk giai bai nay voi a
mn giup mk giai bai nay voi a