cho hình bình hành ABCD có AB=a, AD=b
chứng minh rằng AC2+BD2=2(a2+b2)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
20 tháng 9 2017
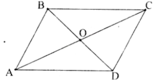
Gọi O là giao điểm của AC và BD ⇒ O là trung điểm của AC và BD.
Xét ΔABC có BO là trung tuyến
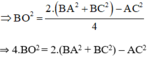
Mà O là trung điểm của BD nên BD = 2. BO ⇒ BD2 = 4. BO2
⇒ BD2 = 2.(AB2 + BC2) – AC2
⇒ BD2 + AC2 = 2.(AB2 + BC2)
⇒ m2 + n2 = 2.(a2 + b2) (ĐPCM).
NQ
1
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 3 2021
Ta có: \(AC^2+BD^2=\left(\overrightarrow{AB}+\overrightarrow{AD}\right)^2+\left(\overrightarrow{BC}+\overrightarrow{BA}\right)^2\)
\(=AB^2+AD^2+2\overrightarrow{AB}.\overrightarrow{AD}+BC^2+BA^2+2\overrightarrow{BA}.\overrightarrow{BC}\)
\(=AB^2+AD^2+BC^2+AD^2+2\overrightarrow{AB}\left(\overrightarrow{AD}-\overrightarrow{BC}\right)\)
\(=AB^2+AD^2+BC^2+AD^2\)
CM
2 tháng 2 2019
a, HS tự chứng minh
b, HS tự chứng minh
c, Chú ý ∆AKD:∆ANC (g.g) và ∆ABI:∆ACM (g.g). Từ đó tính được AD.AN và AB.AM
PT
1
CM
1 tháng 11 2019
Biến đổi vế trái ta có:
VT = ( a 2 + b 2 )( c 2 + d 2 )
= a 2 c 2 + a 2 d 2 + b 2 c 2 + b 2 d 2
= ( a 2 c 2 + 2abcd + b 2 d 2 ) + ( a 2 d2 – 2abcd + b 2 c 2 )
= a c + b d 2 + a d - b c 2 =VP
Vế phải bằng vế trái nên đẳng thức được chứng minh.
11 tháng 4 2022
-Sửa đề: \(\widehat{A}=\widehat{D}=90^0\)
a) -△OAB và △OCD có: \(\widehat{OAB}=\widehat{OCD};\widehat{AOB}=\widehat{COD}\)
\(\Rightarrow\)△OAB∼△OCD (g-g).
b) \(AC^2-BD^2=DC^2-AB^2\)
\(\Leftrightarrow AC^2-DC^2=BD^2-AB^2\)
\(\Leftrightarrow AD^2=AD^2\) (luôn đúng).
c) -△BCD có: OI//DC \(\Rightarrow\dfrac{DC}{OI}=\dfrac{BD}{BO}\Rightarrow\dfrac{DC}{OI}-1=\dfrac{OD}{BO}\)
-△AOB có: AB//DC \(\Rightarrow\dfrac{OD}{BO}=\dfrac{DC}{AB}=\dfrac{DC}{OI}-1\)
\(\Rightarrow\dfrac{DC}{AB}+1=\dfrac{DC}{OI}\Rightarrow\dfrac{DC+AB}{AB}=\dfrac{DC}{OI}\Rightarrow\dfrac{1}{OI}=\dfrac{DC+AB}{DC.AB}=\dfrac{1}{AB}+\dfrac{1}{DC}\)
29 tháng 6 2023
a: Xét ΔHBA vuông tại H và ΔIDC vuông tại I có
BA=DC
góc HAB=góc ICD
=>ΔHBA=ΔIDC
=>AH=IC
b: Xét tứ giác BHDI có
BH//DI
BH=DI
=>BHDI là hình bình hành
c; S CAB=AB*CM/2
S DAC=1/2*CN*AD
mà ΔCAB=ΔDAC
nên AB*CM=CN*AD
- Gọi E là giao điểm của AC và BD
△ABE có trung tuyến BE
\(\Rightarrow BE^2=\dfrac{2\left(AB^2+BC^2\right)-AC^2}{4}\)
\(\Rightarrow4.BE^2=2\left(AB^2+BC^2\right)-AC^2\)
Mà O là trung điểm BD \(\Rightarrow BD=2.BE\Rightarrow BD^2=4.BE^2\)
\(\Rightarrow BD^2=2\left(AB^2+BC^2\right)-AC^2\)
\(\Rightarrow BD^2+AC^2=2\left(AB^2+BC^2\right)\)
Vậy: \(AC^2+BD^2=2\left(a^2+b^2\right)\left(đpcm\right)\)
(Hình như đây là Toán 10?)
Lời giải:
Kẻ đường cao $BH, DT$ của hình bình hành
Dễ chứng minh $\triangle ADT =\triangle BCH$ (ch-gn)
$\Rightarrow DT=CH; AT=BH$
Áp dụng định lý Pitago:
$AC^2+BD^2=AT^2+TC^2+BH^2+DH^2$
$=(AT^2+BH^2)+TC^2+DH^2)$
$=2AT^2+(DC-DT)^2+(DC+CH)^2$
$=2(AD^2-DT^2)+(DC-DT)^2+(DC-DT)^2$
$=2(b^2-DT^2)+(a-DT)^2+(a+DT)^2$
$=2(b^2+a^2)$
Ta có đpcm.