Cho hàm số y = mx^2 - (m + 1)x - 2m + 3. Tìm tập hợp đỉnh của...
Đọc tiếp
Cho hàm số y = mx^2 - (m + 1)x - 2m + 3. Tìm tập hợp đỉnh của (Pm)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 6 2021
\(y=\dfrac{x^2-m^2+2m+1}{x-m}\) đúng không nhỉ?
\(y'=\dfrac{x^2-2mx+m^2-2m-1}{\left(x-m\right)^2}\)
Hàm đồng biến trên các khoảng xác định khi và chỉ khi:
\(x^2-2mx+m^2-2m-1\ge0\) ; \(\forall x\)
\(\Leftrightarrow\Delta'=m^2-\left(m^2-2m-1\right)\le0\)
\(\Leftrightarrow m\le-\dfrac{1}{2}\)
CM
13 tháng 7 2019
Đồ thị của hai hàm số y = mx + 3 và y = (2m + 1)x – 5 là hai đường thẳng cắt nhau khi và chỉ khi:
m ≠ 2m + 1 => m ≠ -1.
Kết hợp với điều kiện trên, ta có:
DD
Đoàn Đức Hà
Giáo viên
8 tháng 10 2021
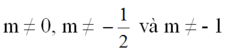
\(y=x^3-mx^2+\left(1-2m\right)x+1\)
\(y'=3x^2-2mx+1-2m\)
Để đồ thị hàm số đã cho có hai cực trị nằm về hai phía của trục tung thì phương trình \(y'=0\)có hai nghiệm phân biệt \(x_1,x_2\)thỏa mãn \(x_1x_2< 0\).
Ta có: \(y'=0\Leftrightarrow3x^2-2mx+1-2m=0\)(1)
Để (1) có hai nghiệm phân biệt thỏa mãn \(x_1x_2< 0\)thì:
\(\hept{\begin{cases}\Delta'=m^2-3\left(1-2m\right)>0\\\frac{1-2m}{3}< 0\end{cases}}\Leftrightarrow m>\frac{1}{2}\).
Vậy \(m>\frac{1}{2}\)thỏa mãn ycbt.
Tọa độ đỉnh P là (-b/2a; -delta/4a)
với y=ax^2+bx+c
Áp dụng vào:
y=mx^2-(m+1)x-2m+3
Delta=(m+1)^2-4m(-2m+3)=m^2+2m+1+8m^2-12m=9m^2-10m+1
a=m,b=-(m+1),c=-2m+3
Là sẽ ra.
Để P(M) đi qua điểm (2,1)=> Thay x=2,y=1 vào cho cái đó =0
2=m-(m+1)-2m+3=>-2m+2=2=>m=0
y=mx^2-(m+1)x-2m+3
mx^2-mx-x-2m+3-y=0
=>m(x^2-x-2)-x-y+3=0
Điểm cố định có tọa độ (x_0,y_0)
Với x_0^2-x_0-2=0 và -x_0-y_0+3=0=>(x_0,y_0)=(2,-1) và (-1,-4)