Cho hình chóp SABCD có đáy ABCD là hình bình hành . Gọi I , J là hai điểm nằm trên SB và SD sao cho SI = 1/3 SB , SJ = 2JD . Tìm giao điểm của :
a) IJ và (ABCD)
b) BJ và (IAC)
c) SA và (ACJ)
d) IJ và (SAC).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
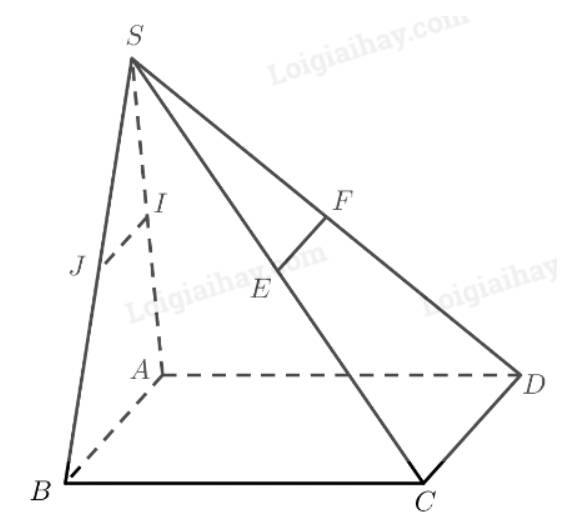
Ta có: \(I\) là trung điểm của \(SA\)
\(J\) là trung điểm của \(SB\)
\( \Rightarrow IJ\) là đường trung bình của tam giác \(SAB\)
\( \Rightarrow IJ\parallel AB\)
\(E\) là trung điểm của \(SC\)
\(F\) là trung điểm của \(SD\)
\( \Rightarrow EF\) là đường trung bình của tam giác \(SC{\rm{D}}\)
\( \Rightarrow EF\parallel C{\rm{D}}\)
Mà \(AB\parallel C{\rm{D}}\).
Vậy \(IJ\parallel EF\parallel AB\parallel C{\rm{D}}\).
Vậy \(AD\) không song song với \(IJ\)
Chọn C.
28 tháng 10 2023
a: \(O\in AC\subset\left(SAC\right);O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SO\)
b: Chọn mp(SAD) có chứa SA
Xét (SAD) và (CKB) có
\(K\in\left(SAD\right)\cap\left(CKB\right)\)
AD//CB
Do đó: (SAD) giao (CKB)=xy, xy đi qua K và xy//AD//CB
Gọi J là giao điểm của SA với xy
=>J là giao điểm của SA với mp(CKB)
c: \(C\in OA\subset\left(OIA\right);C\in\left(SCD\right)\)
=>\(C\in\left(OIA\right)\cap\left(SCD\right)\)
Xét ΔBSD có
O,I lần lượt là trung điểm của BD,BS
=>OI là đường trung bình của ΔBSD
=>OI//SD
Xét (OIA) và (SCD) có
\(C\in\left(OIA\right)\cap\left(SCD\right)\)
OI//SD
Do đó: (OIA) giao (SCD)=mn, mn đi qua C và mn//OI//SD
CM
14 tháng 2 2017
Chọn C.
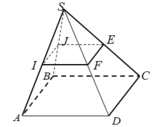
+) Ta có, IJ là đường trung bình tam giác SAB nên IJ // AB. ⇒ D đúng.
+) ABCD là hình bình hành nên AB// CD. Mà IJ// AB
Suy ra , IJ // CD ⇒ B đúng.
+) EF là đường trung bình tam giác SCD nên EF // CD.
Suy ra, IJ // EF ⇒ A. đúng.
- Do đó chọn đáp án C.
ai giúp em với ạ :(