cho các hàm số y=0.5x 3,y=6-x,y=mx có đồ thị lần lượt là các đường thẳng (d1),(d2) và (dentam).với những giá trị nào của tham số m thì đường thẳng (dentam)cắt đường thẳng (d1),(d2) lần lượt ở 2 điểm A và B sao cho A có hoành độ âm còn B có hoành độ dương
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
3 tháng 1 2019
Ta có phương trình hoành độ giao điểm của d 1 v à d 2 : m x – 2 = 1 2 x + 1 ( * )
Để hai đường thẳng d 1 v à d 2 cắt nhau tại một điểm có hoành độ x = − 4 t h ì x = − 4 thỏa mãn phương trình (*)
Suy ra m . ( − 4 ) – 2 = 1 2 . ( − 4 ) + 1 ⇔ − 4 m – 2 = − 2 + 1 ⇔ − 4 m = 1 ⇔ m = 1 4
Đáp án cần chọn là: A
16 tháng 11 2023
a: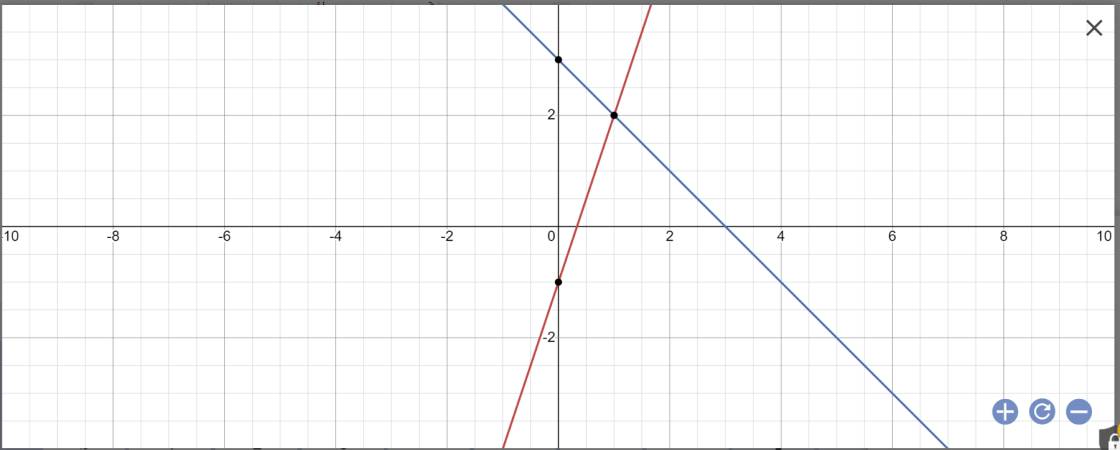 
b: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\3x-1=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{1}{3}\\y=0\end{matrix}\right.\)
Vậy: A(1/3;0)
Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\-x+3=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\-x=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=3\end{matrix}\right.\)
Vậy: B(3;0)
Tọa độ C là:
\(\left\{{}\begin{matrix}3x-1=-x+3\\y=3x-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x=4\\y=3x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\cdot1-1=2\end{matrix}\right.\)
Vậy: C(1;2)
c: Gọi \(\alpha\) là góc tạo bởi (d1) với trục Ox
\(tan\alpha=a=3\)
=>\(\alpha\simeq71^033'\)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
14 tháng 9 2023
d3//d1 => a=2 (b khác 1)
d3 cắt d2 tại điểm có tung độ bằng 2 Thay y=2 vào d2
=> 2=-x+4=> x=2 Thay y=2; x=2; a=2 vào d3
=> 2+2.2+b=> b=-6
11 tháng 8 2021
b) Phương trình hoành độ giao điểm của (D1) và (d2) là:
-x+4=x-4
\(\Leftrightarrow-2x=-8\)
hay x=4
Thay x=4 vào (d1), ta được:
y=-4+4=0
Thay x=0 vào (d1), ta được:
\(y=-0+4=4\)
Thay x=0 vào (d2), ta được:
\(y=0-4=-4\)
Vậy: A(0;4); B(0;-4); C(4;0)