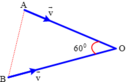
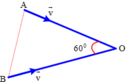
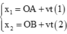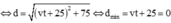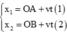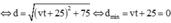1. 2 xe chuyển động trên OA,OB cùng hướng về O với \(v2=\dfrac{v1}{\sqrt{3}}\) . OA và OB hợp với nhau 1 góc 30 độ. Khi khoảng cách giữa 2 xe cực tiểu là d thì khoảng cách từ xe 1 đến O là \(30\sqrt{3}\)m. Tính khoảng cách từ xe 2 đến O.
2. 2 đường thẳng d1 và d2 hợp với nhau 1 góc 60 độ, chúng chuyển động theo các vận tốc v1, v2 theo phương vuông góc với chính nó. Tìm vận tốc giao điểm O của 2 đường thẳng nếu v1=4m/s, v2=3m/s