Giải giúp mk câu 22 vs 23
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(\frac{12}{13}=1-\frac{1}{13}\) ; \(\frac{22}{23}=1-\frac{1}{23}\)
Do \(\frac{1}{13}>\frac{1}{23}\)nên \(1-\frac{1}{13}< 1-\frac{1}{23}\)
Vậy \(\frac{12}{13}< \frac{22}{23}\)
\(\frac{12}{13}=1-\frac{1}{13};\frac{22}{23}=1-\frac{1}{23}\)
Có \(1-\frac{1}{13}< 1-\frac{1}{23}\Rightarrow\frac{12}{13}< \frac{22}{23}\)



Coi A=1+2+22+...+22024
B=5.22023
�=1+2+22+...+22022
A=1+2+22+...+22024�=1+2+22+...+22022
⇒2A=2+22+...+22024⇒2�=2+22+...+22023
⇒2A−A=22024−1⇒2�−�=22023−1
⇒A=22024−1⇒�=22023−1
⇒A<22024=2
.22023=2.22023

a: \(=\left(1+2\right)+2^2\left(1+2\right)+...+2^{48}\left(1+2\right)\)
\(=3\left(1+2^2+...+2^{48}\right)⋮3\)
b: \(2^0+2^1+2^2+...+2^{101}\)
\(=\left(1+2+2^2\right)+...+2^{99}\left(1+2+2^2\right)\)
\(=7\left(1+...+2^{99}\right)⋮7\)
c: 2A=2+2^2+...+2^101
=>A=2^101-1

Ta thấy ràng 34=...1 , mà (......1)k luôn tận cùng là 1=> 4 thừa số 3 cho ta 1 tích tận cùng là 1 ;
- các hạng tử trong A liên tiếp cách đều 10 đơn vị nên :
Số hạng trong A là: (2013 -3):10 +1= 202 số;
=> Chia làm 202 : 4= 50 cặp sô(dư 2);
=> A= ...................1 x 3 x 3 =....................9;
Vậy A tận cùng là 9;
Xét B, ta có: 24=...6 , mà (...6)k luôn tận cùng là 6, nên
B có : (2012-2) : 10 +1 = 202 số hạng;
Chia làm : 202 : 4= 50 cặp (dư 2);
=> B=.................6 x 2 x 2=...............4;
=> A-B=......................9-........................4=.......................5;
Vậy x chia hết cho 5


\(=\left(\dfrac{2-\sqrt{3}+1}{2}\right):\left(\dfrac{\sqrt{3}-1+4}{2}\right)=\left(\dfrac{3-\sqrt{3}}{2}\right):\left(\dfrac{3+\sqrt{3}}{2}\right)\)
\(=\dfrac{3-\sqrt{3}}{3+\sqrt{3}}=\dfrac{\left(3-\sqrt{3}\right)^2}{\left(3+\sqrt{3}\right)\left(3-\sqrt{3}\right)}=\dfrac{12-6\sqrt{3}}{6}=2-\sqrt{3}\)
\(\left(1-\dfrac{\sqrt{3}-1}{2}\right):\left(\dfrac{\sqrt{3}-1}{2}+2\right)\)
\(=\dfrac{3-\sqrt{3}}{2}:\dfrac{\sqrt{3}-3}{2}\)
=-1



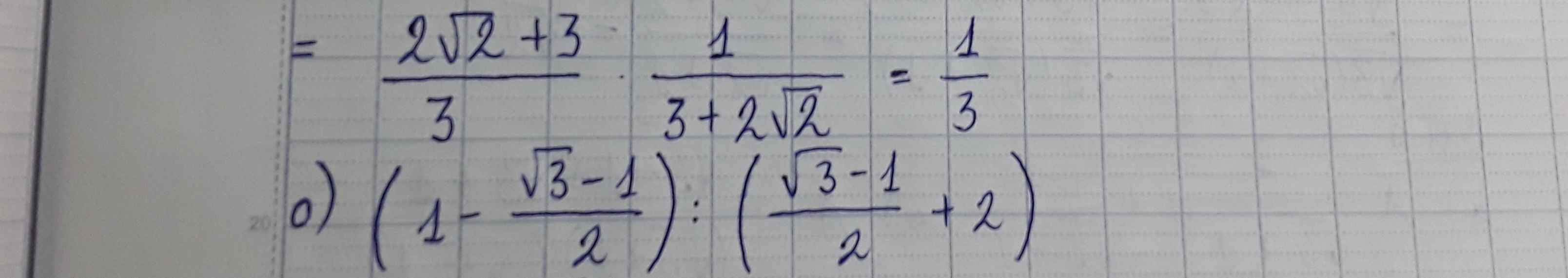 giải giúp mk câu o vs ạ
giải giúp mk câu o vs ạ
22. Ta có: \(\dfrac{32}{3,5}\le p\le\dfrac{32}{3}\)
\(\Rightarrow p=10\)
\(\Rightarrow n_X=32-2p=32-2.10=12\)
\(\Rightarrow A_X=p+n_X=12\)
Theo đề, tổng số hạt trong X nhiều hơn Y 2 hạt
mà \(p_X=p_Y=10\)(Vì X và Y là 2 đồng vị của R)
\(\Rightarrow n_Y=n_X-2=12-2=10\)
\(\Rightarrow A_Y=p+n_Y=10+10=20\)
Ta có: \(\overline{A_R}=\dfrac{22.45+20.455}{45+455}=20,18\)