Giải giúp em với E đang cần gấp!!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Bài 1:
1: \(\sqrt{3+2\sqrt{2}}=\sqrt{2}+1\)
2: \(\sqrt{5-2\sqrt{6}}=\sqrt{3}-\sqrt{2}\)
3: \(\sqrt{11-2\sqrt{30}}=\sqrt{6}-\sqrt{5}\)
4: \(\sqrt{7-2\sqrt{10}}=\sqrt{5}-\sqrt{2}\)

1) \(\sqrt{2x-5}=7\)
\(\left(\sqrt{2x-5}\right)^2=7^2\)
\(2x-5=49\)
\(2x=54\)
\(x=27\)
2) \(3+\sqrt{x-2}=4\)
\(\sqrt{x-2}=1\)
\(\left(\sqrt{x-2}\right)^2=1^2\)
\(x-2=1\)
\(x=3\)
1) \(\sqrt{2x-5}=7\left(đk:x\ge\dfrac{5}{2}\right)\)
\(\Leftrightarrow2x-5=49\Leftrightarrow2x=54\Leftrightarrow x=27\left(tm\right)\)
2) \(3+\sqrt{x-2}=4\left(đk:x\ge2\right)\)
\(\Leftrightarrow\sqrt{x-2}=1\Leftrightarrow x-2=1\Leftrightarrow x=3\)
3) \(\Leftrightarrow\sqrt{\left(x-1\right)^2}=1\Leftrightarrow\left|x-1\right|=1\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=1\\x-1=-1\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=0\end{matrix}\right.\)
4) \(\Leftrightarrow\sqrt{\left(x-2\right)^2}=1\Leftrightarrow\left|x-2\right|=1\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=1\\x-2=-1\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=1\end{matrix}\right.\)
5) \(\Leftrightarrow\sqrt{\left(2x-1\right)^2}=\sqrt{\left(x+4\right)^2}\)
\(\Leftrightarrow\left|2x-1\right|=\left|x+4\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=x+4\\2x-1=-x-4\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)
6) \(ĐK:x\ge-2\)
\(\Leftrightarrow5\sqrt{x+2}-3\sqrt{x+2}-\sqrt{x+2}=\sqrt{x+7}\)
\(\Leftrightarrow\sqrt{x+2}=\sqrt{x+7}\)
\(\Leftrightarrow x+2=x+7\Leftrightarrow2=7\left(VLý\right)\)
Vậy \(S=\varnothing\)
7) \(ĐK:x\ge-1\)
\(\Leftrightarrow5\sqrt{2x+1}+3\sqrt{x+1}=4\sqrt{x+1}+4\sqrt{2x+1}\)
\(\Leftrightarrow\sqrt{2x+1}=\sqrt{x+1}\)
\(\Leftrightarrow2x+1=x+1\Leftrightarrow x=0\left(tm\right)\)

Dài đấy bạn nên chia nhỏ ra để nhận được câu tl nhanh nhất nhé :v
Mình làm bài 1
`a)x=1/2`
`<=>Q=(4.1/2)/(1/4-1)`
`=2/(-3/4)=-8/3`
`b)P=(x+1)/(x-1)+x/(x+1)-x/(x^2-1)`
`=((x+1)^2+x(x-1)-x)/(x^2-1)`
`=(x^2+2x+1+x^2-x-x)/(x^2-1)`
`=(2x^2+1)/(x^2-1)`
`c)A=P:Q=(2x^2+1)/(x^2-1).(x^2-1)/(4x)`
`=(2x^2+1)/(4x)`
`A=3/4`
`<=>8x^2+4=4x`
`<=>2x^2+1=3x`
`<=>2x^2-3x+1=0`
`<=>(x-1)(2x-1)=0`
`<=>x=1\or\x=1/2`
Vậy...

a: góc AEH=góc ADH=góc DAE=90 độ
=>AEHD là hcn
b: XétΔAEH vuông tại E và ΔAHC vuông tại H có
góc EAH chung
=>ΔAEH đồng dạng với ΔAHC
c: ΔAHC vuông tại H có HE là đường cao
nên HE^2=AE*EC

Câu 2:
a, Vì m⊥MN và n⊥MN nên m//n
b, Vì m//n nên \(\widehat{D_1}=\widehat{C}=45^0\) (so le trong)
c, Vì m//n nên \(\widehat{D_1}=\widehat{C_1}\) (đồng vị)

Câu 1:
uses crt;
var a:array[1..100]of integer;
i,n,min:integer;
begin
clrscr;
write('Nhap n='); readln(n);
for i:=1 to n do
begin
write('A[',i,']='); readln(a[i]);
end;
min:=a[1];
for i:=1 to n do
if min>a[i] then min:=a[i];
writeln(min);
readln;
end.
Câu 2:
uses crt;
var st:string;
begin
clrscr;
write('Nhap xau:'); readln(st);
writeln('Xau ',st,' co ',length(st),' phan tu');
readln;
end.





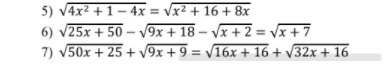







 giải giúp e với ạ đang cần gấp!!
giải giúp e với ạ đang cần gấp!!