Tìm GTLN của biểu thức sau :
\(D=3-\dfrac{5}{2}\left|\dfrac{2}{5}-x\right|\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 10 2021
\(a,A=\dfrac{x-9-x+4+\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}:\dfrac{x-2-x+\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\\ A=\dfrac{\sqrt{x}-3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\cdot\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\sqrt{x}}\\ A=\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
17 tháng 4 2022
B1: ĐXXĐ: \(x\ne\pm2;x\ne-1\)
\(=\left(\dfrac{x-2}{\left(x+2\right)\left(x-2\right)}-\dfrac{2\left(x+2\right)}{\left(x+2\right)\left(x-2\right)}+\dfrac{x}{\left(x+2\right)\left(x-2\right)}\right):\dfrac{-6\left(x+2\right)}{\left(x-2\right)\left(x+1\right)}\)
\(=\left(\dfrac{x-2-2x-2+x}{\left(x+2\right)\left(x-2\right)}\right):\dfrac{-6\left(x+2\right)}{\left(x-2\right)\left(x+1\right)}\)
\(=\dfrac{-4}{\left(x+2\right)\left(x-2\right)}:\dfrac{-6\left(x+2\right)}{\left(x-2\right)\left(x+1\right)}\)
\(=\dfrac{-4}{\left(x+2\right)\left(x-2\right)}.\dfrac{\left(x-2\right)\left(x+1\right)}{-6\left(x+2\right)}=\dfrac{2\left(x+1\right)}{3\left(x+2\right)^2}\)
b, \(A=\dfrac{2\left(x+1\right)}{3\left(x+2\right)^2}>0\)
\(\Leftrightarrow2x+2>0\) (vì \(3\left(x+2\right)^2\ge0\forall x\))
\(\Leftrightarrow x>-1\).
-Vậy \(x\in\left\{x\in Rlx>-1;x\ne2\right\}\) thì \(A>0\).
5 tháng 11 2023
a: A>0
=>\(x^2-3x>0\)
=>x(x-3)>0
TH1: \(\left\{{}\begin{matrix}x>0\\x-3>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>0\\x>3\end{matrix}\right.\)
=>x>3
TH2: \(\left\{{}\begin{matrix}x< 0\\x-3< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< 0\\x< 3\end{matrix}\right.\)
=>x<0
d: Để D<0 thì \(x^2+\dfrac{5}{2}x< 0\)
=>\(x\left(x+\dfrac{5}{2}\right)< 0\)
TH1: \(\left\{{}\begin{matrix}x>0\\x+\dfrac{5}{2}< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>0\\x< -\dfrac{5}{2}\end{matrix}\right.\)
=>Loại
Th2: \(\left\{{}\begin{matrix}x< 0\\x+\dfrac{5}{2}>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< 0\\x>-\dfrac{5}{2}\end{matrix}\right.\)
=>\(-\dfrac{5}{2}< x< 0\)
e: ĐKXĐ: x<>2
Để E<0 thì \(\dfrac{x-3}{x-2}< 0\)
TH1: \(\left\{{}\begin{matrix}x-3>=0\\x-2< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=3\\x< 2\end{matrix}\right.\)
=>Loại
TH2: \(\left\{{}\begin{matrix}x-3< =0\\x-2>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< =3\\x>2\end{matrix}\right.\)
=>2<x<=3
g: Để G<0 thì \(\left(2x-1\right)\left(3-2x\right)< 0\)
=>\(\left(2x-1\right)\left(2x-3\right)>0\)
TH1: \(\left\{{}\begin{matrix}2x-1>0\\2x-3>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>\dfrac{1}{2}\\x>\dfrac{3}{2}\end{matrix}\right.\)
=>\(x>\dfrac{3}{2}\)
TH2: \(\left\{{}\begin{matrix}2x-1< 0\\2x-3< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< \dfrac{1}{2}\\x< \dfrac{3}{2}\end{matrix}\right.\)
=>\(x< \dfrac{1}{2}\)
28 tháng 7 2023
a: \(A=\dfrac{x-2-2x-4+x}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{-\left(x-2\right)\left(x+1\right)}{6\left(x+2\right)}\)
\(=\dfrac{-6}{\left(x+2\right)}\cdot\dfrac{-\left(x+1\right)}{6\left(x+2\right)}=\dfrac{\left(x+1\right)}{\left(x+2\right)^2}\)
b: A>0
=>x+1>0
=>x>-1
c: x^2+3x+2=0
=>(x+1)(x+2)=0
=>x=-2(loại) hoặc x=-1(loại)
Do đó: Khi x^2+3x+2=0 thì A ko có giá trị
12 tháng 1 2023
a: ĐKXĐ: x<>1; x<>2; x<>3
\(K=\left(\dfrac{x^2}{\left(x-2\right)\left(x-3\right)}+\dfrac{x^2}{\left(x-1\right)\left(x-2\right)}\right)\cdot\dfrac{\left(x-1\right)\left(x-3\right)}{x^4+2x^2+1-x^2}\)
\(=\dfrac{x^3-x^2+x^3-3x^2}{\left(x-2\right)\left(x-3\right)\left(x-1\right)}\cdot\dfrac{\left(x-1\right)\left(x-3\right)}{\left(x^2+1+x\right)\left(x^2+1-x\right)}\)
\(=\dfrac{2x^3-4x^2}{\left(x-2\right)}\cdot\dfrac{1}{\left(x^2+x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{2x^2\left(x-2\right)}{\left(x-2\right)\left(x^4+x^2+1\right)}=\dfrac{2x^2}{x^4+x^2+1}\)
b:
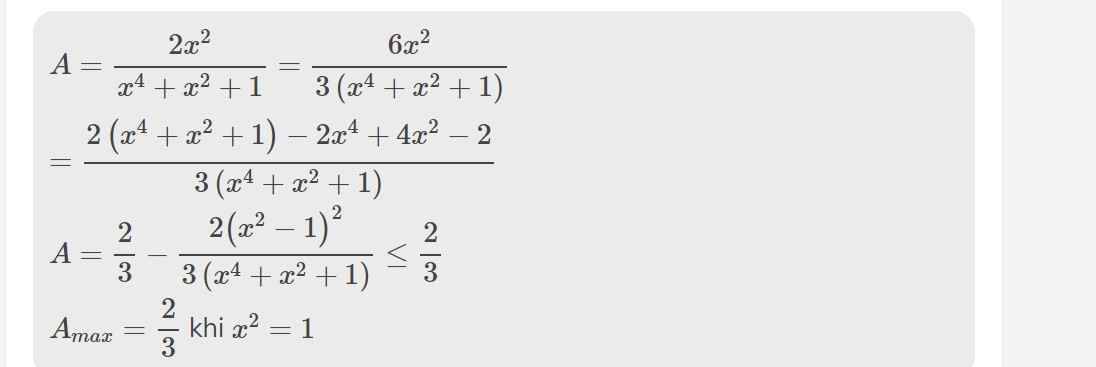
Ta có:
\(D=3-\dfrac{5}{2}\left|\dfrac{2}{5}-x\right|\)
mà \(\left|\dfrac{2}{5}-x\right|\ge0\)
\(\Leftrightarrow\dfrac{5}{2}\left|\dfrac{2}{5}-x\right|\ge0\)
\(\Leftrightarrow D\le3\)
Để D đạt GTLN thì \(\left|\dfrac{2}{5}-x\right|\) phải đạt GTNN
Dấu '' = '' xảy ra khi:
\(\left|\dfrac{2}{5}-x\right|=0\)
\(\Leftrightarrow x=\dfrac{2}{5}\)
Vậy ......
Chúc bạn học tốt!
Phạm Hoàng GiangNguyễn Thanh HằngLinh NguyễnNguyễn Huy Tú
và các bạn nữa!