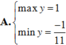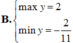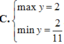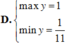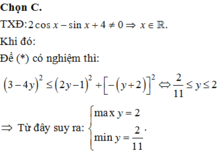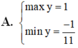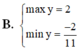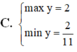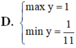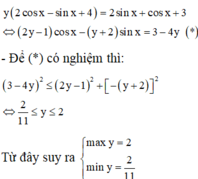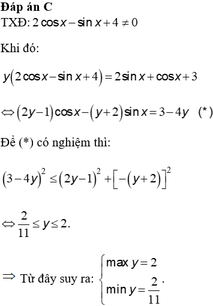Tìm các GTLN của hàm số y = 2sinx - 4/3sin^3x trên [0;π]
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
1 tháng 4 2018
Xét hàm số y=2sin x + cos 2x trên đoạn
y’=2cos x- 2sin 2x = 2cos x(1- 2sin x)
Trên đoạn [0; π]
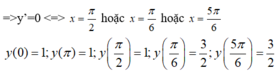
Giá trị lớn nhất của hàm số này trên [0; π] là y = 3 2 .
Chọn B
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 7 2021
\(y=\left|2sin^2x-sinx-1\right|-2sinx\)
Đặt \(sinx=t\in\left[-1;1\right]\)
\(\Rightarrow y=f\left(t\right)=\left|2t^2-t-1\right|-2t\)
BBT cho \(f\left(t\right)\) trên \(\left[-1;1\right]\):
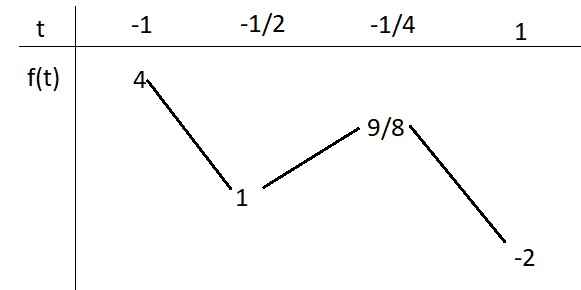
Từ BBT ta thấy \(y_{max}=4\) khi \(sinx=-1\); \(y_{min}=-2\) khi \(sinx=1\)
.
.
.
.
CM
13 tháng 4 2019
Chọn A
Điều kiện: 
. Điều kiện cần để hàm số 
nghịch biến trên khoảng 
là
.
Ta có :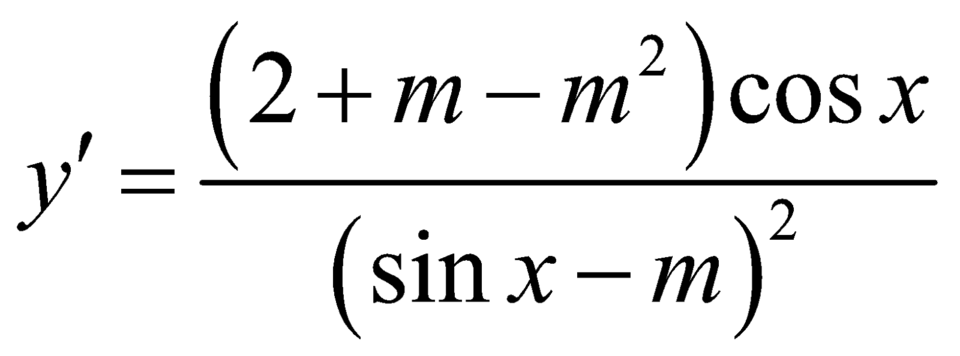 
.
Ta thấy 
.
Để ham số 
nghịch biến trên khoảng 
là
.
CM
16 tháng 3 2018
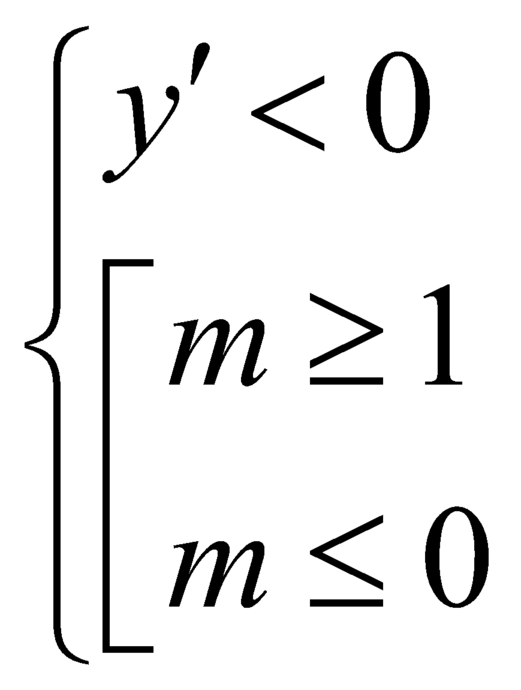
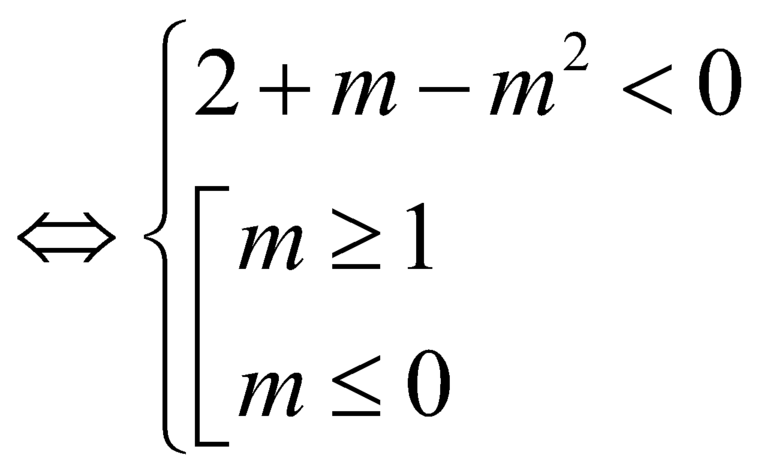
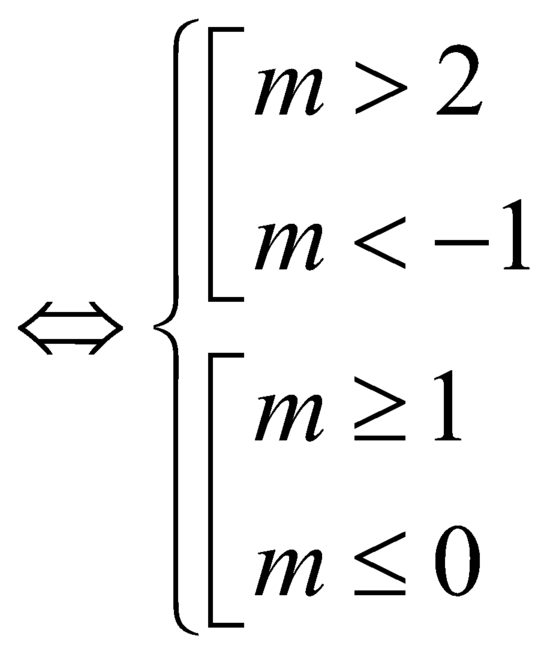
a) 
f′(x) > 0 trên khoảng (-4; 0) và f’(x) < 0 trên khoảng (0; 4).
Hàm số đạt cực đại tại x = 0 và f C Đ = 5
Mặt khác, ta có f(-4) = f(4) = 3
Vậy 
d) f(x) = | x 2 − 3x + 2| trên đoạn [-10; 10]
Khảo sát sự biến thiên và vẽ đồ thị của hàm số g(x) = x 2 – 3x + 2.
Ta có:
g′(x) = 2x − 3; g′(x) = 0 ⇔ x = 3/2
Bảng biến thiên:
Vì
nên ta có đồ thị f(x) như sau:
Từ đồ thị suy ra: min f(x) = f(1) = f(2) = 0; max = f(x) = f(−10) = 132
e) 
f′(x) < 0 nên và f’(x) > 0 trên (π/2; 5π/6] nên hàm số đạt cực tiểu tại x = π/2 và f C T = f(π/2) = 1
Mặt khác, f(π/3) = 2√3, f(5π/6) = 2
Vậy min f(x) = 1; max f(x) = 2
g) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]
f′(x) = 2cosx + 2cos2x = 4cos(x/2).cos3(x/2)
f′(x) = 0
⇔ 
Ta có: f(0) = 0,
Từ đó ta có: min f(x) = −2 ; max f(x) = 3√3/2
NL
2
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 11 2021
\(y=4\left(1-sin^2x\right)+2sinx+2=-4sin^2x+2sinx+6\)
Đặt \(sinx=t\in\left[-1;1\right]\Rightarrow y=f\left(t\right)=-4t^2+2t+6\)
\(-\dfrac{b}{2a}=\dfrac{1}{4}\in\left[-1;1\right]\)
\(f\left(-1\right)=0\) ; \(f\left(\dfrac{1}{4}\right)=\dfrac{25}{4}\); \(f\left(1\right)=4\)
\(\Rightarrow y_{max}=\dfrac{25}{4}\) khi \(sinx=\dfrac{1}{4}\)
\(y_{min}=0\) khi \(sinx=-1\)
1 tháng 11 2021
Ta có: \(y=4cos^2x+2sinx+2=4-4sin^2x+2sinx+2=-4sin^2x+2sinx+6=-\left(4sin^2x-2sinx+\dfrac{1}{16}-\dfrac{1}{16}-6\right)=-\left(2sin^2x-\dfrac{1}{4}\right)^2+\dfrac{97}{16}\)
Ta có: \(-\left(2sin^2x-\dfrac{1}{4}\right)^2\le0\Rightarrow y\le\dfrac{97}{16}\)
Vậy \(y_{max}=\dfrac{97}{16}\)