Hai thị trấn A,B cách nhau 22km/h bằng một con đường bằng một đoạn dốc lên và một đoạn dốc xuống. Một người đi xe đạp từ thị trấn A sang thị trấn B, mất 1h 10ph. Biết rằng tốc đọ của anh lúc lên dốc là 15km/h và xuống dốc là 24km/h, hãy tính độ dài đoạn đường dốc lên và dốc xuống.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tóm tắt:
s = 22 km
t = 1 giờ 10 phút = \(\frac{7}{6}\) giờ
v1 = 15 km/h
v2 = 24 km/h
_____________________
s1 = ? (km)
s2 = ? (km)
Giải:
Gọi t1 và t2 theo thứ tự là thời gian lên dốc và thời gian xuống dốc.
\(\Rightarrow t_2=t-t_1=\frac{7}{6}-t_1\left(h\right)\)
Quãng đường lên dốc:
\(v_1=\frac{s_1}{t_1}\Rightarrow s_1=v_1\times t_1=15t_1\left(km\right)\)
Quãng đường xuông dốc:
\(v_2=\frac{s_2}{t_2}\Rightarrow s_2=v_2\times t_2=24\times\left(\frac{7}{6}-t_1\right)=28-24t_1\left(km\right)\)
Ta có:
\(s_1+s_2=s\)
\(15t_1+28-24t_1=22\)
\(24t_1-15t_1=28-22\)
\(9t_1=6\)
\(t_1=\frac{6}{9}=\frac{2}{3}h\)
Quãng đường lên dốc:
\(v_1=\frac{s_1}{t_1}\Rightarrow s_1=v_1\times t_1=15\times\frac{2}{3}=10\left(km\right)\)
Quãng đường xuống dốc:
\(s=s_1+s_2\Rightarrow s_2=s-s_1=22-10=12\left(km\right)\)
ĐS: 10 km và 12 km

1h57,5p = \(\dfrac{47}{24}\)h
1h50p = \(\dfrac{11}{6}\)h
Nếu khi đi người đó lên dốc đoạn S1 và xuống đoạn S2 thì khi về người đó xuống dốc đoạn S1 và lên dốc đoạn S2
=> \(\dfrac{S_1}{18}\) + \(\dfrac{S_2}{24}\) = \(\dfrac{47}{24}\)h
=> \(\dfrac{S_1}{24}\) + \(\dfrac{S_2}{18}\) = \(\dfrac{11}{6}\)
Cộng vế vs v
\(\dfrac{S_1}{18}\) + \(\dfrac{S_2}{24}\) + \(\dfrac{S_1}{24}\) + \(\dfrac{S_2}{18}\) = \(\dfrac{91}{24}\)
⇒ \(\dfrac{S_1+S_2}{18}\) + \(\dfrac{S_1+S_2}{24}\) = \(\dfrac{91}{24}\)
⇒ \(\dfrac{4\left(S_1+S_2\right)}{72}\) + \(\dfrac{3\left(S_1+S_2\right)}{72}\) = \(\dfrac{273}{72}\)
⇒ 4(S1 + S2) + 3(S1 + S2) = 273
⇒ 7(S1 + S2) = 273
⇒ S1 + S2 =39
Vậy 2 xã cách nhau 39km

Gọi x (km) là độ dài quãng đường AM (x > 0)
Gọi y (km) là độ dài quãng đường BM (y > 0)
Thời gian đi từ A đến B: \(\dfrac{x}{9}+\dfrac{y}{18}=2\) (1)
Thời gian đi từ B về A: \(\dfrac{x}{18}+\dfrac{y}{9}=3\) (2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{x}{9}+\dfrac{y}{18}=2\\\dfrac{x}{18}+\dfrac{y}{9}=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+y=36\\x+2y=54\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x+2y=72\\x+2y=54\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x=18\\2x+y=36\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=6\left(nhận\right)\\2.6+y=36\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=6\left(nhận\right)\\y=24\left(nhận\right)\end{matrix}\right.\)
Vậy AM = 6 km, MB = 24 km

Gọi vận tốc lúc lên dốc và vận tốc lúc xuống dốc theo thứ tự là x, y (km/h) (x, y > 0)
* Lúc đi từ A đến B: Đoạn lên dốc dài 4km và đoạn xuống dốc dài 5km
* Lúc đi từ B đến A: Đoạn lên dốc dài 5 km và đoạn xuống dốc dài 4 km
Thời gian đi lên dốc là 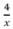 ( h) , thời gian xuống dốc là:
( h) , thời gian xuống dốc là: 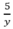 (h)
(h)
Theo đầu bài thời gian đi A đến B là 40 phút = 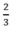 h nên:
h nên:
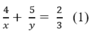
* Lúc đi từ B đến A qua C: Đoạn lên dốc dài 5 km và đoạn xuống dốc dài 4 km
Thời gian đi lên dốc là 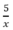 ( h) , thời gian xuống dốc là:
( h) , thời gian xuống dốc là: 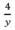 (h)
(h)
Theo đầu bài thời gian đi A đến B là 41 phút = 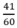 h nên:
h nên:
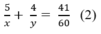
Từ (1) và (2) ta có hệ phương trình:
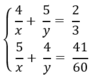
Đặt 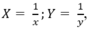 hệ phương trình trên trở thành:
hệ phương trình trên trở thành:
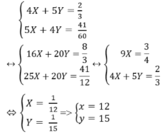
Vậy vậy tốc độ lúc lên dốc là 12km/h, vận tốc lúc xuống dốc là 15km/h.

Gọi vận tốc lúc lên dốc và vận tốc lúc xuống dốc theo thứ tự là x, y (km/h) (x, y > 0)
* Lúc đi từ A đến B: Đoạn lên dốc dài 4km và đoạn xuống dốc dài 5km
* Lúc đi từ B đến A: Đoạn lên dốc dài 5 km và đoạn xuống dốc dài 4 km
Thời gian đi lên dốc là 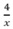 ( h) , thời gian xuống dốc là:
( h) , thời gian xuống dốc là: 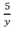 (h)
(h)
Theo đầu bài thời gian đi A đến B là 40 phút = 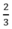 h nên:
h nên:
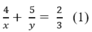
* Lúc đi từ B đến A qua C: Đoạn lên dốc dài 5 km và đoạn xuống dốc dài 4 km
Thời gian đi lên dốc là 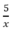 ( h) , thời gian xuống dốc là:
( h) , thời gian xuống dốc là: 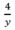 (h)
(h)
Theo đầu bài thời gian đi A đến B là 41 phút = 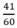 h nên:
h nên:
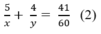
Từ (1) và (2) ta có hệ phương trình:
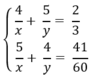
Đặt 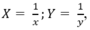 hệ phương trình trên trở thành:
hệ phương trình trên trở thành:
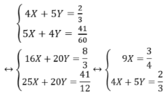
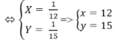
Vậy vậy tốc độ lúc lên dốc là 12km/h, vận tốc lúc xuống dốc là 15km/h.

Gọi vận tốc lúc lên dốc và vận tốc lúc xuống dốc theo thứ tự là x, y (km/h) (x, y > 0)
Vậy vậy tốc độ lúc lên dốc là 12km/h, vận tốc lúc xuống dốc là 15km/h.

đổi 1h10 phút = 7/6 h
Gọi quãng đường lên dốc là s1, quãng đường xuống dốc là s2. ta có :
Thời gian lên dốc và xuống dốc lần lượt là :
t1 = \(\dfrac{s_1}{v_1}\) = \(\dfrac{s_1}{15}\)
t2 = \(\dfrac{s_2}{v_2}\) = \(\dfrac{s_2}{24}\)
mà t1 + t2 = t = 7/6h = \(\dfrac{s_1}{15}\) + \(\dfrac{s_2}{24}\) = \(\dfrac{s_1}{15}\) + \(\dfrac{22-s_1}{24}\) =\(\dfrac{24s_1+330-15s_1}{360}\) = \(\dfrac{9s_1+330}{360}\)
=> 9s1 + 330 = 360 . 7/6
=> 9s1 = 90
=> s1 = 90/9 = 10 (km)
=> s2 = 22 - 10 = 12 (km)
vậy độ dài đoạn đường xuống dốc là : 12 km
đoạn đường xuống dốc là : 10km