Hình thang vuông ABCD ( \(\widehat{A}=\widehat{D}=90^o\) ) có BC = 10cm, M và N theo thứ tự là các trung điểm của AD và BC, khoảng cách từ M đến BC bằng nửa AD. Tính độ dài MN.
~ Ai biết chỉ liền hộ tớ ạ :) Cảm ơn ~
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 11 2022
Kẻ MH vuông góc với BC
=>MN là khoảng cách từ M đến BC
Theo đề, ta có: MH=MA=MD=AD/2
=>ΔHAD vuông tại H
Xét ΔMDC vuông tại D và ΔMHC vuông tại H có
MC chung
MD=MH
Do đó: ΔMDC=ΔMHC
=>CD=CH
Xét ΔMAB vuông tại A và ΔMHB vuông tại H có
MH chung
MA=MH
Do đó: ΔMAB=ΔMHB
=>AB=BH
HB+HC=BC
=>AB+DC=BC
=>AB+DC=10cm
=>MN=1/2(AB+CD)=5cm
9 tháng 10 2017
1) a) Do ABCD là hình thang cân => góc D = góc C ; góc B = góc A
Trong t/g ABC có : góc A = 90 độ => góc D + góc C2 = 90 độ
Trong t/g ABC có AB = BC ( gt ) => t/g ABC cân tại B => góc A1 = góc C1
Ta có góc A = 90 độ + góc A1 = góc D + góc C2 + góc C1 = góc C + góc C = 2C
Mà :
A + B + C + D = 360 độ = 2A + 2C = 4C + 2C = 6C => góc C = 360 độ : 6 = 60 độ
=> góc C = góc D ( = 60 độ ) ; góc A = góc B ( = 120 độ )
22 tháng 11 2022
Kẻ MH vuông góc với BC
=>MN là khoảng cách từ M đến BC
Theo đề, ta có: MH=MA=MD=AD/2
=>ΔHAD vuông tại H
Xét ΔMDC vuông tại D và ΔMHC vuông tại H có
MC chung
MD=MH
Do đó: ΔMDC=ΔMHC
=>CD=CH
Xét ΔMAB vuông tại A và ΔMHB vuông tại H có
MH chung
MA=MH
Do đó: ΔMAB=ΔMHB
=>AB=BH
HB+HC=BC
=>AB+DC=BC
=>AB+DC=10cm
=>MN=1/2(AB+CD)=5cm
22 tháng 11 2022
Kẻ MH vuông góc với BC
=>MN là khoảng cách từ M đến BC
Theo đề, ta có: MH=MA=MD=AD/2
=>ΔHAD vuông tại H
Xét ΔMDC vuông tại D và ΔMHC vuông tại H có
MC chung
MD=MH
Do đó: ΔMDC=ΔMHC
=>CD=CH
Xét ΔMAB vuông tại A và ΔMHB vuông tại H có
MH chung
MA=MH
Do đó: ΔMAB=ΔMHB
=>AB=BH
HB+HC=BC
=>AB+DC=BC
=>AB+DC=10cm
=>MN=1/2(AB+CD)=5cm
CM
30 tháng 6 2019
Chọn B.
Phương pháp:
Gắn hệ trục tọa độ.
Cách giải:
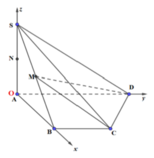
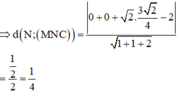
Vây, khoảng cách từ N đến mặt phẳng (MCD) bằng: 1 4 a
22 tháng 11 2022
Bạn đổi E thành M, F thành N nha
Kẻ MH vuông góc với BC
=>MN là khoảng cách từ M đến BC
Theo đề, ta có: MH=MA=MD=AD/2
=>ΔHAD vuông tại H
Xét ΔMDC vuông tại D và ΔMHC vuông tại H có
MC chung
MD=MH
Do đó: ΔMDC=ΔMHC
=>CD=CH
Xét ΔMAB vuông tại A và ΔMHB vuông tại H có
MH chung
MA=MH
Do đó: ΔMAB=ΔMHB
=>AB=BH
HB+HC=BC
=>AB+DC=BC
=>AB+DC=10cm
=>MN=1/2(AB+CD)=5cm