K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 3 2022
Gọi x là qđ AB (km)
Vận tốc đi là \(25\left(\dfrac{km}{h}\right)\)
Vận tốc về là \(30\left(\dfrac{km}{h}\right)\)
Thời gian đi là \(\dfrac{x}{25}\left(h\right)\)
Thời gian về là \(\dfrac{x}{30}\left(h\right)\)
20p = 1/3(h)
Do thời gian về ít hơn lúc đi là 20p nên ta có
\(\dfrac{x}{25}-\dfrac{x}{30}=\dfrac{1}{3}\\ \Leftrightarrow30x-25x=\dfrac{1}{3}\\ \Leftrightarrow5x=\dfrac{1}{3}\\ \Leftrightarrow x=15\)
21 tháng 3 2022
Cách giải đây nhé!
Gọi thời gian lúc đi là x(x>0) (h)
Đổi 20 phút = 1/3 giờ
Do thời gian về ít hơn thời gian đi là 20 phút nên thời gian lúc về là x−1/3
Do quãng đường không đổi nên ta có phương trình :
25x= 30(x−1/3)
⇔ 25x= 30x−10
⇔ −5x= −10
9 tháng 7 2024
1.
Đáp số : Các số là : 1884 ; 1882 ; 1880 ; 1888 ; 1890 ; 1892 .
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
9 tháng 7 2024
Bài 1:
Giải:
Trung bình cộng của 7 số chẵn liên tiếp cũng là trung bình cộng của số đầu và số thứ bảy của dãy đó và bằng 18
Tổng của số đầu và số thứ bảy là: 18 x 2 = 36
Hiệu của số thứ nhất và số thứ bảy là: 2 x (7 - 1) = 12
Số thứ nhất là: (36 - 12) : 2 = 12
Số thứ nhất là số chẵn vậy không có 7 số lẻ liên tiếp nào thoả mãn đề bài
11 tháng 10 2021
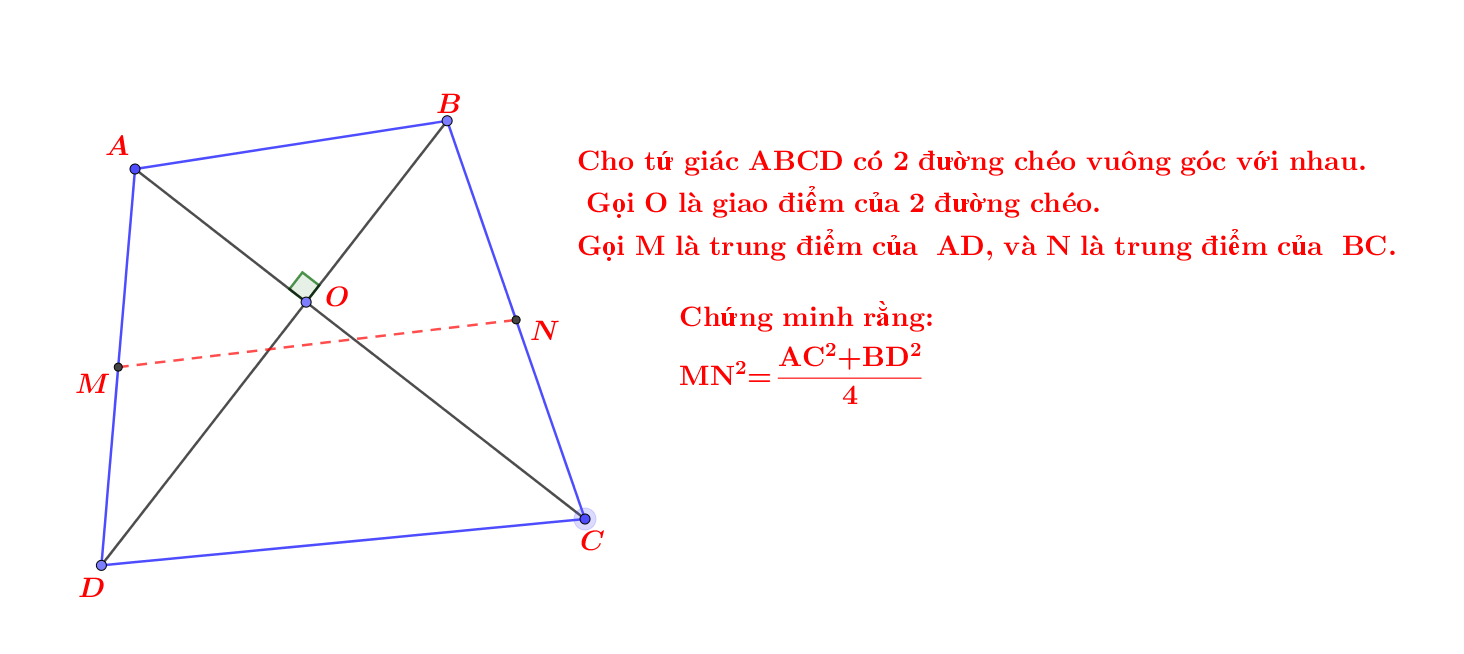
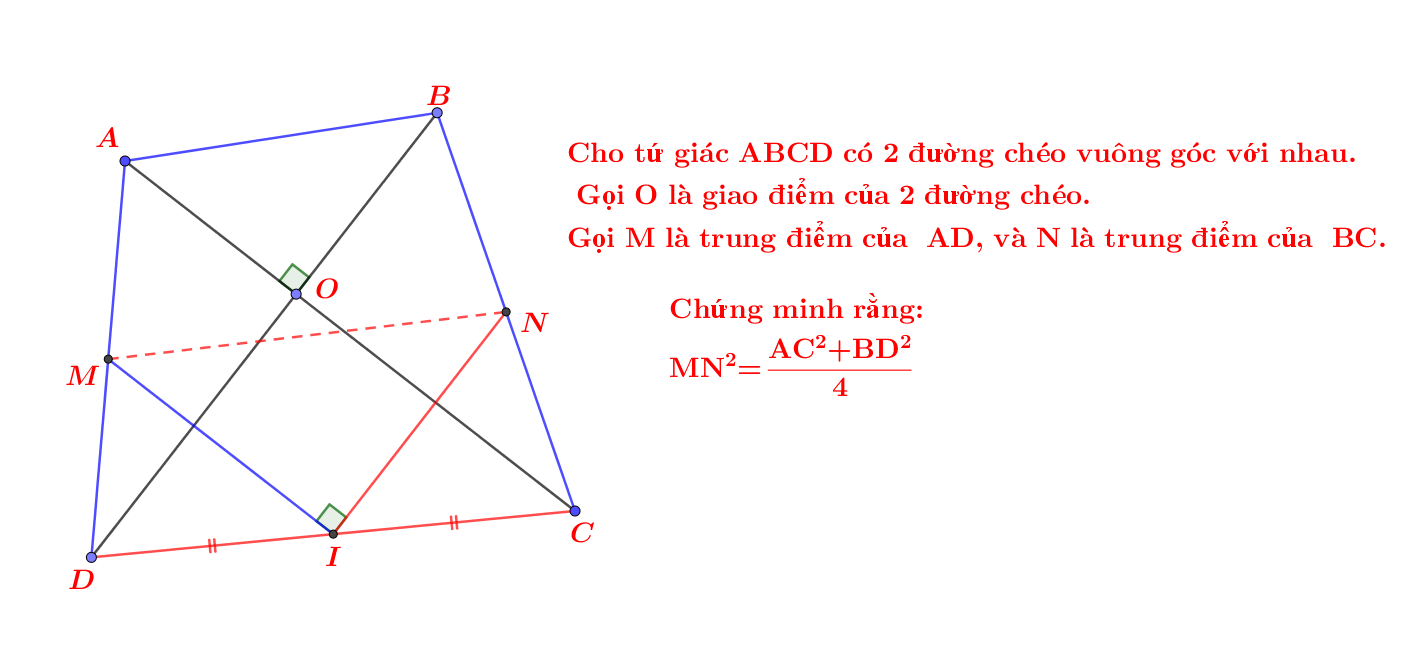
Ta có: MN là đường trung bình
nên MN//CD
mà CD\(\perp\)AH
nên AH\(\perp\)MN
11 tháng 10 2021
Ta có:MN là đường trung bình của ΔACD
⇒MN//CD
mà AH⊥CD(đường cao AH)
⇒AH⊥MN
11 tháng 10 2021
Xét tam giác ACD có:
MN là đường trung bình
=> MN//CD
Mà AH⊥CD(AH là đường cao)
=> AH⊥MN(từ vuông góc đến song song)
TT
14 tháng 3 2021
Đổi : 30 phút = 0,5 giờ
Gọi quãng đường AB là x ( km )
ĐK : x > 0
Thời gian lúc đi là : \(\dfrac{x}{50}\left(h\right)\)
Thời gian lúc về là : \(\dfrac{x}{60}\left(h\right)\)
Thời gian về ít hơn thời gian đi là 30 phút, nên ta có phương trình :
\(\dfrac{x}{50}-\dfrac{x}{60}=0,5\)
\(\Leftrightarrow\left(\dfrac{1}{50}-\dfrac{1}{60}\right)x=0,5\)
\(\Leftrightarrow\dfrac{1}{300}x=0,5\)
\(\Leftrightarrow x=0,5\div\dfrac{1}{300}\)
\(\Leftrightarrow x=150\) ( thỏa mãn điều kiện )
Vậy quãng đường AB dài 150 km.
6 tháng 10 2023
Số thứ ba là:
\(4270:5=854\)
Trung bình cộng của 3 số đầu là số thứ hai.
Số thứ hai là:
\(854-1=853\)
Đáp số: 853