Cho x+y=5. Tính giá trị của biểu thức:
M= x3+y3 -2(x2+ y2) +3xy(x+y) - 4xy + 3x + 10 +3y
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

`#3107.101107`
`D = x^3 - y^3 - 3xy` biết `x - y - 1 = 0`
Ta có:
`x - y - 1 = 0`
`=> x - y = 1`
`D = x^3 - y^3 - 3xy`
`= (x - y)(x^2 + xy + y^2) - 3xy`
`= 1 * (x^2 + xy + y^2) - 3xy`
`= x^2+ xy + y^2 - 3xy`
`= x^2 - 2xy + y^2`
`= x^2 - 2*x*y + y^2`
`= (x - y)^2`
`= 1^2 = 1`
Vậy, với `x - y = 1` thì `D = 1`
________
`E = x^3 + y^3` với `x + y = 5; x^2 + y^2 = 17`
`x + y = 5`
`=> (x + y)^2 = 25`
`=> x^2 + 2xy + y^2 = 25`
`=> 2xy = 25 - (x^2 + y^2)`
`=> 2xy = 25 - 17`
`=> 2xy = 8`
`=> xy = 4`
Ta có:
`E = x^3 + y^3`
`= (x + y)(x^2 - xy + y^2)`
`= 5 * [ (x^2 + y^2) - xy]`
`= 5 * (17 - 4)`
`= 5 * 13`
`= 65`
Vậy, với `x + y = 5; x^2 + y^2 = 17` thì `E = 65`
________
`F = x^3 - y^3` với `x - y = 4; x^2 + y^2 = 26`
Ta có:
`x - y = 4`
`=> (x - y)^2 = 16`
`=> x^2 - 2xy + y^2 = 16`
`=> (x^2 + y^2) - 2xy = 16`
`=> 2xy = (x^2 + y^2) - 16`
`=> 2xy = 26 - 16`
`=> 2xy = 10`
`=> xy = 5`
Ta có:
`F = x^3 - y^3`
`= (x - y)(x^2 + xy + y^2)`
`= 4 * [ (x^2 + y^2) + xy]`
`= 4 * (26 + 5)`
`= 4*31`
`= 124`
Vậy, với `x - y = 4; x^2 + y^2 = 26` thì `F = 124.`

\(a,A=x^2+y^2\\=x^2-2xy+y^2+2xy\\=(x-y)^2+2xy\\=2^2+2\cdot1\\=4+2\\=6\)
\(b,x+y=1\\\Leftrightarrow (x+y)^3=1^3\\\Leftrightarrow x^3+3x^2y+3xy^2+y^3=1\\\Leftrightarrow x^3+3xy(x+y)+y^3=1\\\Leftrightarrow x^3+3xy\cdot1+y^3=1\\\Rightarrow A=1\)
a) Ta có:
\(x-y=2\)
\(\Rightarrow\left(x-y\right)^2=2^2\)
\(\Rightarrow x^2-2xy+y^2=4\)
Mà: \(xy=1\)
\(\Rightarrow\left(x^2+y^2\right)-2\cdot1=4\)
\(\Rightarrow x^2+y^2=4+2\)
\(\Rightarrow x^2+y^2=6\)
b) Ta có:
\(x+y=1\)
\(\Rightarrow\left(x+y\right)^3=1^3\)
\(\Rightarrow x^3+3x^2y+3xy+y^3=1\)
\(\Rightarrow x^3+3xy\left(x+y\right)+y^3=1\)
Mà: x + y = 1
\(\Rightarrow x^3+3xy\cdot1+y^3=1\)
\(\Rightarrow x^3+3xy+y^3=1\)

Câu 1: x^3+y^3+3xy
=(x+y)^3-3xy(x+y)+3xy
=(x+y)^3-3xy+3xy
=1
Câu 2:
x^3-y^3-3xy
=(x-y)^3+3xy(x-y)-3xy
=1^3
=1
Câu 3:
\(x^2+y^2=\left(x+y\right)^2-2xy=4-2\cdot\left(-15\right)=4+30=34\)
Câu 4:
\(x^3+y^3=\left(x+y\right)^3-3xy\left(x+y\right)=-8-3\cdot\left(-2\right)\cdot\left(-15\right)=-8-3\cdot30=-98\)
Câu 5: B
Câu 6: C
Câu 7: B
Câu 8: D
Câu 10: B
1) Nếu x+y=1, thì giá trị của biểu thức x3+y3+3xy là
A.2
B.3
C.4
D.cả A,B,C đều sai
2)Nếu x-y=1, thì giá trị của biểu thức x3-y3-3xy là
A.1
B.2
C.3
D.4
3) Cho x+y= -2, xy=-15 thì giá trị của biểu thức x2+y2 là.
A) 30 ; B) 32 ;C) 28 ; D) Cả A và B đều sai.
4) Với giả thiết bài 3, ta có giá trị của biểu thức x3+y3 là:
A) 80 ; B) 81; C) 82 ; D) Một kết quả khác
5) Với giả thiết bài 3, ta có giá trị của biểu thức x4+y4 là:
A. 706 ; B. 702 ; C. 708 ; D. 704
6)Giá trị nhỏ nhất của biểu thức P= x(x+1)(x+2)(x+3) là
A. 1 ; B. 2 ; C. -1 ; D.-2
7)Cho biểu thức M=2x2+9y2- 6xy-6x-12y+2037 . Giá trị nhỏ nhất của biểu thức M là
A. 2007 ; B. 2008 ; C; 2009 ; D. 2010
8) Với giả thiết bài 7 , biểu thức M đạt giá trị nhỏ nhất khi
A)x=5;y= 7/3
B)x= -5; y= 7/3
C) x=5; y= -7/3
D)cả A và C đều sai
9) Cho biểu thức Q= 2xy+6x-2y-2x2-y2+ 2015 .Giá trị lớn nhất của biểu thức Q là
A. 2010 ; B. 2012 ; C. 2020 ; D. Một kết quả khác

\(P=\left(x+2y\right)^2-2\left(x+2y\right)\left(y-1\right)+\left(y-1\right)^2\\ P=\left(x+2y-y+1\right)^2=\left(x+y+1\right)^2\\ Q.sai.đề\\ M=\left(x+y\right)^3-3xy\left(x+y\right)+3xy\\ M=1^3-3xy\left(x+y-1\right)=1-3xy\left(1-1\right)=1-0=1\\ x+y=2\Leftrightarrow\left(x+y\right)^2=4\\ \Leftrightarrow x^2+y^2+2xy=4\\ \Leftrightarrow2xy=4-10=-6\\ \Leftrightarrow xy=-3\\ N=x^3+y^3=\left(x+y\right)\left(x^2-xy+y^2\right)\\ N=2\left(10+3\right)=2\cdot13=26\)

Ta có: \(x-y=5\Rightarrow\left(x-y\right)^2=25\)
\(\Rightarrow x^2+y^2-2xy=25\)
\(\Rightarrow15-2xy=25\)
\(\Rightarrow2xy=-10\Rightarrow xy=-5\)
\(M=x^3-y^3=\left(x-y\right)\left(x^2+xy+y^2\right)=5\left(15-5\right)=5.10=50\)

Chọn B.
P =
2
(
x
3
+
y
3
)
-
3
x
y
![]()
![]() (do
x
2
+
y
2
=
2
)
(do
x
2
+
y
2
=
2
)
Đặt x + y = t. Ta có
x
2
+
y
2
=
2
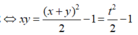
Từ ![]()
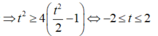
P = f(t) 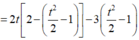
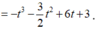
Xét f(t) trên [-2;2].
Ta có ![]()
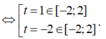
Bảng biến thiên
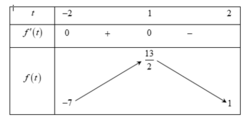
Từ bảng biến thiên ta có max P = max f(t) = 13 2 ; min P = min f(t) = -7
Lời bình: Có thể thay bbt thay bằng
Ta có ![]()
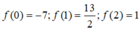
Suy ra kết luận.
\(M=x^3+y^3-2\left(x^2+y^2\right)+3xy\left(x+y\right)-4xy+3x+10+3y\)
\(=x^3+y^3-2x^2-2y^2+3x^2y+3xy^2-4xy+3x+10+3y\)
\(=\left(x^3+3x^2y+3xy^2+y^3\right)-2\left(x^2+2xy+y^2\right)+3\left(x+y\right)+10\)
\(=\left(x+y\right)^3-2\left(x+y\right)^2+3\left(x+y\right)+10\)
Ta có: x + y = 5
\(\Rightarrow\left(x+y\right)^3-2\left(x+y\right)^2+3\left(x+y\right)+10=5^3-2.5^2+3.5+10=125-50+15+10=100\)
Vậy M = 100.