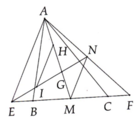
Cho tam giác ABC có trọng tâm G. Gọi H là điểm đối xứng của B qua G
a. Chứng minh và
b. Gọi M là trung điểm BC. Chứng minh
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

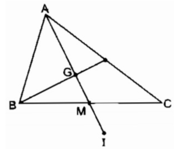
I đối xứng với A qua tâm G
ta có: GA = GI, GM ∈ GA ( tính chất đường trung tuyến của tam giác)
Suy ra: GM ∈ GI
Mà: GM + MI = GI và GM = AG/2 (tính chất đường trung tuyến) =>GM = GI/2
Suy ra: GM = MI nên điểm M là trung điểm của GI
Vậy I đối xứng với G qua M.

a: góc BEC=góc BDC=90 độ
=>BEDC nội tiếp
b: góc HBC+góc HCB=90 độ-góc ABC+90 độ-góc ACB
=góc BAC
=>góc BHC=180 độ-góc BAC
=>góc BHC+góc BAC=180 độ
H đối xứng M qua BC
=>BH=BM và CH=CM
Xét ΔBHC và ΔBMC có
BH=BM
HC=MC
BC chung
=>ΔBHC=ΔBMC
=>góc BMC=góc BHC
=>góc BMC+góc BAC=180 độ
=>ABMC nội tiếp
c: Xét tứ giác BHCN có
BC cắt HN tại trung điểm của mỗi đường
=>BHCN là hìnhbình hành
=>góc BHC=góc BNC
=>góc BNC+góc bAC=180 độ
=>ABNC nội tiếp

Vì G là trọng tâm \(\Delta ABC\) (gt)
\(\Rightarrow MG=\dfrac{1}{2}GA=\dfrac{1}{2}GI\) (t/c trọng tâm)
\(\Rightarrow\) MG = MI
\(\Rightarrow\) M là trung điểm của GI (ĐN trung điểm)
\(\Rightarrow\) I đối xứng với G qua M (ĐN đối xứng tâm)

a: Xét tứ giác BPNC có
G là trung điểm của BN
G là trung điểm của PC
Do đó: BPNC là hình bình hành